Glossar - Begriffe rund um Graphen
Begriffsklärungen schaffen Klarheit
Wenn man mit Graphen arbeitet, ergeben sich von selbst eine Vielzahl neuer Begriffe.
So wird im Kontext Graphen
häufig von gerichteten Kanten, Nachbarn, Wegen und Kreisen gesprochen.
Vieler dieser Begriffe werden intuitiv verstanden, da sie analog in unserer Alltagswelt verwendet werden. So ist recht klar, was man unter einem Weg innerhalb eines Graphen versteht. Nicht ganz so klar ist dagegen der Begriff des Kreises.
In einer Fachwissenschaft wie der Informatik verlässt man sich nicht auf ein intuitives Verständnis von Begriffen, sondern schafft Klarheit und Eindeutigkeit durch Begriffsdefinitionen.
Im Folgenden sollen Begriffe zusammengestellt werden, die in den weiteren Abschnitten benötigt werden.
Graphentypen
Die Beispiele der vorangegangenen Abschnitte lassen bereits verschiedene Typen von Graphen erkennen.
In einem ungerichteten Graphen beschreiben die Kanten eine symmetrische Beziehung: Wenn Objekt A in Beziehung zu Objekt B steht, dann steht auch Objekt B in Beziehung zu Objekt A. Kanten in ungerichteten Graphen werden durch Linien dargestellt.
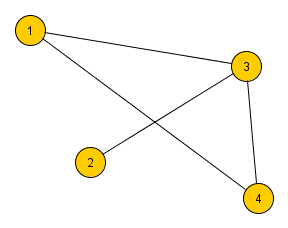
Aufgabe 1
Beschreibe ein Anwendungsbeispiel, in dem man einen ungerichteten Graphen zur Darstellung der vernetzten Struktur benutzt.
In einem gerichteten Graphen beschreiben die Kanten eine asymmetrische Beziehung (bei der gilt: Wenn Objekt A in Beziehung zu Objekt B steht, dann muss Objekt B nicht unbedingt auch in Beziehung zu Objekt A stehen). Kanten in gerichteten Graphen werden durch Pfeile dargestellt.
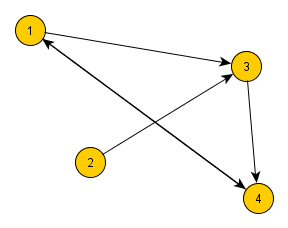
Aufgabe 2
Beschreibe ein Anwendungsbeispiel, in dem man einen gerichteten Graphen zur Darstellung der vernetzten Struktur benutzt.
In einem gewichteten Graphen sind die (gerichteten oder ungerichteten) Kanten mit Zusatzinformationen (meist in Form von Zahlen) versehen.
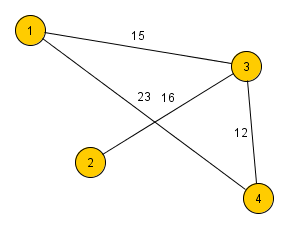
Aufgabe 3
Beschreibe ein Anwendungsbeispiel, in dem man einen gewichteten Graphen zur Darstellung der vernetzten Struktur benutzt.
In einem Multigraphen können Knoten über mehrere Kanten miteinander verbunden werden.
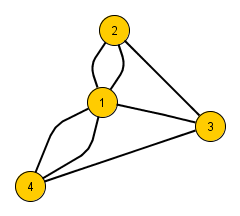
Aufgabe 4
Beschreibe ein Anwendungsbeispiel, in dem man einen Multigraphen zur Darstellung der vernetzten Struktur benutzt.
Nachbarn, Wege, Zyklen, ...
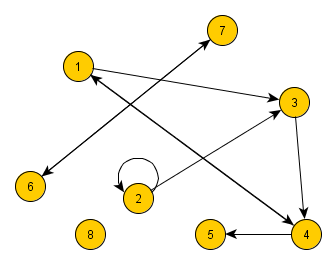
Ist in einem gerichteten Graphen ein Knoten über eine Kante mit einem anderen Knoten verbunden, so heißen diese andere Knoten Nachbarn des Ausgangsknoten.
In ungerichteten Graphen sind zwei Knoten Nachbarn, wenn sie über eine Kante miteinander verbunden sind.
Aufgabe 5
Welche Nachbarn hat Knoten 1 (Knoten 2) im Beispielgraphen?
Ein Knoten, der keine Nachbarn hat, wird auch isolierter Knoten genannt.
Aufgabe 6
Gibt es im Beispielgraphen einen isolierten Knoten?
Ein Weg innerhalb eines Graphen ist eine Folge von Knoten des Graphen, die sukzessive über eine Kante miteinander verbunden sind.
Aufgabe 7
Verdeutliche am Beispielgraphen den Weg [1,4,1,3,2,2].
Ein Kreis ist ein Weg, bei dem nur Start- und Endknoten identisch sind.
Aufgabe 8
Gib es Kreise im Beispielgraphen? Wenn ja, welche?

