Geheimnisteilen
Eine geometrische Variante des Geheimnisteilens
In der bisher kennengelernten Variante des Geheimnisteilens waren die Teilgeheimnisse untereinander nicht verflochten und bei der Kenntnis aller Teilgeheimnisse könnte das Geheimnis selbst unmittelbar bestimmt werden. Ein geometrischer Ansatz zum Geheimnisteilen baut auf dem Wissen der Geometrie auf, und zwar auf der Tatsache, dass Geraden durch zwei Stützstellen bereits vollständig bestimmt sind.Geraden
Eine Gerade wird durch eine lineare Funktion der Form f(x) = ax+b beschrieben. Als Beispiel betrachten wir die Gerade g, die durch die lineare Funktion f(x) = 2x+1 gegeben ist.
Das folgende Bild zeigt den zur Geraden g gehörigen Funktionsgraphen:
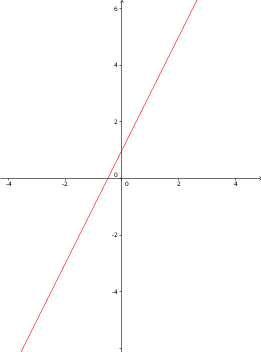
Sind nun zwei Funktionswerte von f bekannt, etwa f(1) = 3 und f(2) = 5, so lässt sich die obige Funktionsvorschrift f(x) = 2x+1 wie folgt bestimmen:
- Bestimmung der Steigung der Geraden g: a1 = = = 2.
- Damit folgt nun die Bestimmung des y-Achsenabschnittes der Geraden g: a0 = f(1) - a1 ⋅ 1 = 1
Es ist also möglich aus der Kenntnis von zwei Stützstellen, also den Wertepaaren ( 1 , f(1) ) und ( 2 , f(2) ), bestehend aus Funktionsargument und zugehörigem Funktionswert, die Funktionsvorschrift zu bestimmen und anschließend alle Werte der Funktion zu berechnen, insbesondere den y-Achsenabschnitt, also den Funktionswert zum Argument x = 0.
Nun gehen wir andersherum vor und beginnen mit einem y-Achsenabschnitt, den wir frei wählen können. Dieser Wert wird später unser Geheimnis sein. Jetzt wird noch eine Steigung gewählt, so ist dadurch eine Gerade eindeutig festgelegt. Nun bestimmen wir zwei Stützstellen dieser Geraden, die dann die beiden Teilgeheimnisse sind.
Der oben dargestellte Rechenweg beschreibt, wie dann mit dem Wissen der beiden Teilgeheimnisse das Geheimnis ermittelt werden kann.
Ein erstes Beispiel
Wir sind nun in der Rolle der Geheimnishüterin und wollen das Geheimnis G = 12, also die Zahl 12, auf zwei Personen aufteilen.
Wir wählen uns als Steigung a1=-4 und damit erhalten wir die Funktionsvorschrift f(x) = -4x+12.
Um zwei Stützstellen zu bestimmen sind nun noch zwei beliebige Argumente (x-Werte) zu wählen, seien diese erneut x1 = 1 und x2 = 2. Zu diesen beiden Argumenten berechnen wir die zugehörigen Funktionswerte f(1) = 8 und f(2) = 4.
Jetzt können wir die beiden Teilgeheimnisse angeben. Das erste Teilgeheimnis ist G1 = ( 1 , f(1) ) = ( 1 , 8 ) und G2 = ( 2 , f(2) ) = ( 2 , 4 ).

