Lösung mit einem genetischen Algorithmus

Der Natur eine Lösungsstrategie abschauen

Wie optimiert die Natur die Anpassung von Lebewesen an Umweltbedingungen? Evolution spielt in den Erklärungsmodellen der Biologen eine wesentliche Rolle. Diese Erklärungsmodelle werden in vielen Biologie-Büchern erklärt, aber z.B. auch in einem Wikipedia-Artikel (vgl. Wikipedia - Evolution).

Die Informatik hat sich die grundlegenden Prinzipien der heutigen Fassung der Evolutionstheorie als Beispiel genommen und sehr stark vereinfacht (Generell nutzt Informatik sehr gerne stark vereinfachte Modelle aus der Biologie.) Die Grundidee wird im folgenden dargestellt:

Zu jedem Zeitpunkt hat man eine Menge von irgendwelchen Lebewesen. Die Lebewesen werden als Individuen bezeichnet, die Menge als Population. Die einzelnen Individuen haben unterschiedliche Eigenschaften. Diese sind in der Erbinformation des Individuums gespeichert, in der Regel in Form von DNA-Molekülen.

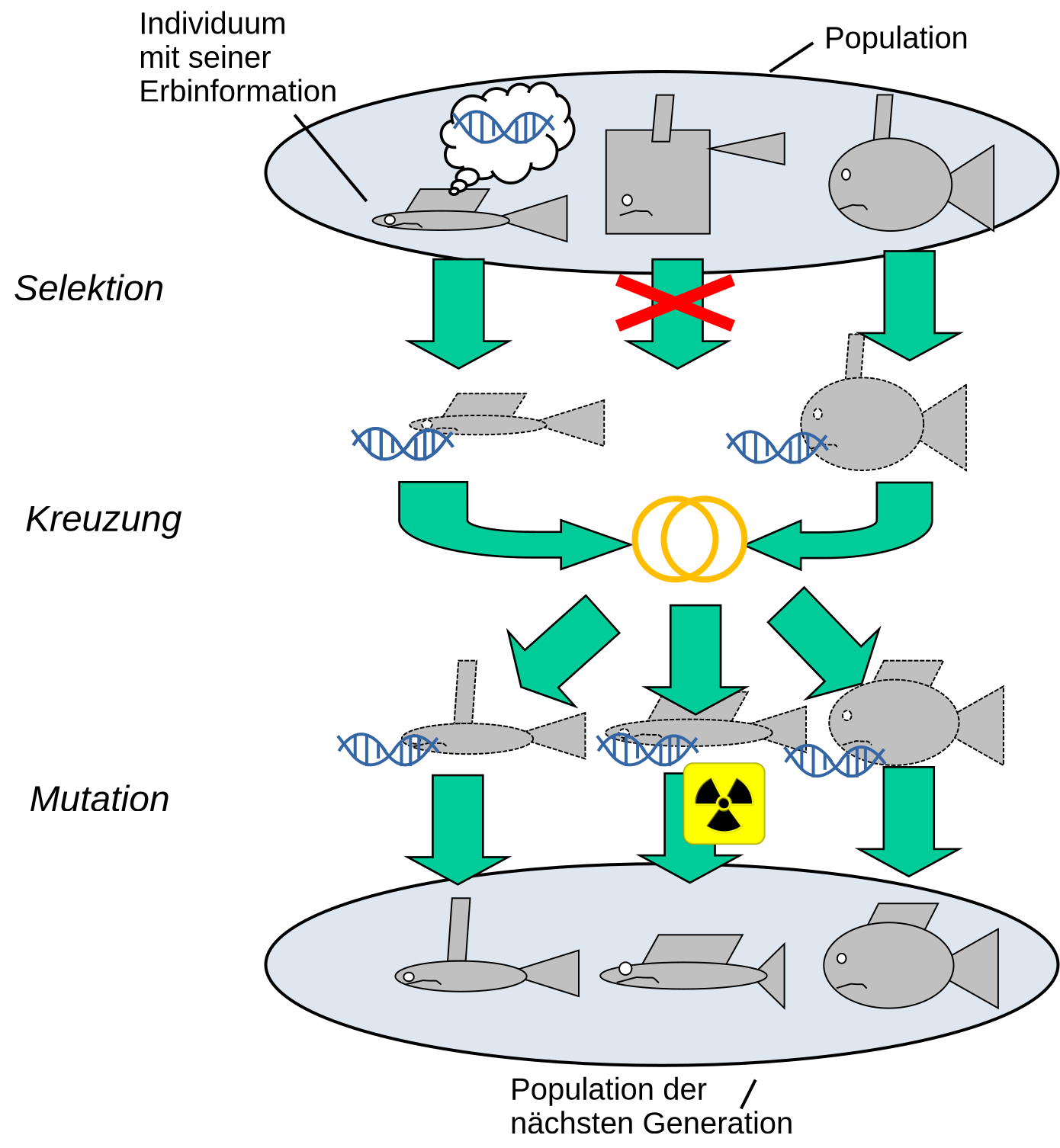
In der Graphik besteht die Population der Übersichtlichkeit halber aus nur drei Fischen als Individuen und nur für eines der Individuen ist die Erbinformation eingezeichnet, obwohl natürlich jedes Individuum seine eigene Erbinformation hat. Aus dieser bestehenden Population entsteht in drei Schritten eine neue Population, die mit großer Wahrscheinlichkeit auch Individuen umfasst, die es in der vorhergehenden Population so nicht gab, die aber trotzdem eine gewisse Ähnlichkeit besitzen.

• Selektion (Auswahl) Von den Individuen sind manche besser an ihren Lebensraum angepasst, manche weniger gut. Dementsprechen sind manche eher in der Lage, ihre Erbinformation (oder Teile davon) an mehr Nachkommen weiterzugeben als andere. In der Graphik ist ein Extremfall gezeigt: der sehr eckige Fisch in der Mitte hat gar keine Nachkommen, vielleicht weil der sich seiner viereckigen Form wegen nicht gut durchs Wasser bewegen kann. Die anderen beiden Fische geben Teile ihrer Erbinformation weiter.
• Rekombination (Kreuzung) Die Erbinformation der erfolgreichen Individuen wird im nächsten Schritt miteinander zur Erbinformation von neuen Individuuen kombiniert. In der Biologie erben die Nachkommen in aller Regel Informationen von zwei Individuuen. Dies Neu-Kombination von Erbinformation kann für die Entwicklung von besonders gut angepassten Individuen sehr wichtig sein, denn es können sich vorteilhafte Eigenschaften von beiden Elternteilen in einem gemeinsamen Nachkommen wiederfinden.
• Mutation (zufällige Veränderung) Nicht alle Erbinformationen der Elternteile werden aber notwendigerweise genauso in die Nachkommen übernommen. Es schleichen sich dabei kleine Kopierfehler ein. Was zunächst wie ein Nachteil klingt, kann für die langfristige Entwicklung insgesamt ein Vorteil sein, denn es können so komplett neuartige Eigenschaften entstehen. Diese werden zwar nicht unbedingt vorteilhaft sein (sie sind ja rein zufällig entstanden), aber es besteht zumindest eine bestimmte Chance dafür.

Das Ergebnis ist eine neue Population von Individuen, die wahrscheinlich im Schnitt etwas besser angepasst sind als die Individuen in der Vorgängerpopulation. Auf diese neue Population wirken dann wieder die Mechanismen von Selektion, Kreuzung und Mutation.

Evolutionäre Algorithmen als Optimierungsmethode

Bei evolutionären oder genetischen Algortignmen werden - motiviert von der biologischen Evolutionstheorie - Individuen (genauer genommen: ihre Erbinformation) als Variablen modelliert und die jeweilige Population als Liste von solchen Variablen. Werden evolutionäre Algorithmen zur Optimierung bestimmter Lösungen verwendet, entspricht ein Individuum einer möglichen Lösung (man sagt: einem Lösungskandidat). Wir werden dieses Vorgehen im Folgenden anhand des Rucksackproblems erläutern, wobei wir der bei der Erläuterung der Übersichtlichkeit halber ein Rucksackproblem mit 10 möglichen Gegenständen betrachten; ihre eigentliche Stärke spielen evolutionäre Algorithmen erst bei viel größeren Problemen aus, wie wir später sehen werden.

Zur Lösung des Rucksackproblems kommen eine Vielzahl an Lösungskandidaten in Frage.

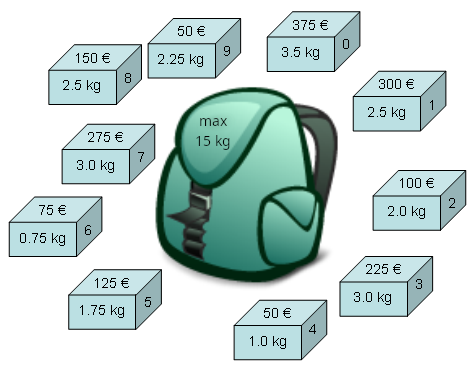
In dem durch die Abbildung gezeigten konkreten Fall wird ein möglicher Lösungskandidat durch eine Auswahl an Gegenständen gegeben, z.B. durch die Gegenstände 0, 2, 3, 4, 5, 8. Wir stellen Lösungskandidaten durch 0-1-Zeichenketten dar. Der Lösungskandidat, der durch die Gegenstände 0, 2, 3, 4, 5, 8 festgelegt wird, wird beispielsweise in der Form '1011110010' dargestellt. In der Biologie entspricht diese Zeichenkette in etwa der Erbinformation.

Eine Population in einem evolutionären Algorithmus zum Rucksackproblem besteht demnach aus einer Liste von 0-1-Zeichenketten. In der Regel gibt man die Größe der Population (d.h. die Länge der Liste) fest vor.

Die folgende Population zum Rucksackproblem besteht aus 8 Individuen, die über ihre jeweilige Erbinformation eine bestimmte Kombination möglicher Gegenstände beschreiben. Beachte, dass zwei Individuen auch dieselbe Erbinformation haben können und somit auch dieselbe Kombination an Gegenständen erfassen können.

'1011110010' 
'0000110010'
'1011010111' 
'1000010010' 
'1010010010' 
'1011110111' 
'1011110010' 
'1010111000'

Fitness von Individuen

Wie oben beschrieben, sind in der Evolution nicht alle Individuen gleichermaßen gut an ihre Umgebung angepasst. Bei informatischen Optimierungsproblemen modelliert man diese "Angepasstheit" über eine so genannte Fitness-Funktion, die jeder Erbinformation einen bestimmten Zahlenwert, eben seiner Fitness, zuordnet. Je höher dieser Zahlenwert ist, desto fitter ist das zugehörige Individuum. Die Fitness beim Rucksackproblem wird so modelliert, dass die Summe aller Werte der Gegenstände des jeweiligen Lösungskandidaten ermittelt wird. Dies gilt aber nur, wenn das Gesamtgewicht unter einem maximale zulässigen Höchstwert bleibt.

Wir legen daher die Fitness eines Lösungskandidaten beim Rucksackproblem wie folgt fest: Wenn die Summe der Gewichte der ausgewählten Gegenstände die Kapazitätsgrenze des Rucksacks nicht übertrifft, so wird Gesamtwert der Gegenstände als Fitnesswert des Lösungskandidaten angesehen. Ansonsten soll der Fitnesswert des Lösungskandidaten 0 betragen.

Aufgabe 1

Bestimme die Fitness der Individuen der folgenden Population unter Berücksichtigung der Vorgaben, die durch das konkrete Rucksackproblem (siehe Abbildung oben, wenn das maximal zulässige Gesamtgewicht 15 kg beträgt) gegeben sind. Welches Individuum ist am fittesten?

 
'1011110010' 
'0000110010' 
'1011010111' 
'1000010010'
'1010010010' 
'1011110111' 
'1011110010' 
'1010111000' 
'1111111111'
 

Selektion

Welche Individuen sollen zur Fortpflanzung beitragen? Wenn das Ziel das Finden eines optimal gepackten Rucksacks ist, ist es nachvollziehbar, dass vor allem die Lösungskandidaten mit einem hohen Fitness-Wert bevorzugt werden.

In unserem Fall modellieren wir die Selektion folgendermaßen

• Wir wählen zwei Individuen der Population zufällig aus und bestimmen ihren jeweiligen Fitness-Wert.
• Dann lassen wir die beiden Individuen in einer Art Turnier gegeneinander antreten: Das Individuum mit der höheren Fitness, der Gewinner trägt zur nächsten Generation bei, das andere nicht.

Man spricht in der Informatik bei einer solchen Modellierung von Selektion tatsächlich von Turnier-Selektion.

Aufgabe 2

Du hast in Aufgabe 1 die Fitness der einzelnen Individuen bestimmt. Wähle nun zufällig vier davon aus und lasse jeweils zwei in einer Turnier-Selektion gegeneinander antreten. Bestimme die beiden Gewinner.

Kreuzung

Die Erzeugung von neuen Individiuen soll durch Kreuzung von zwei Lösungskandidaten realisiert werden. Hierzu wird zunächst eine zufällige Stelle in 0-1-Zeichenkette bestimmt (z.B. die Stelle 7). Die Abschnitte der beiden Zeichenketten werden jetzt (über Kreuz) neu kombiniert. Der 1. Abschnitt des ersten Individuums wird mit dem 2. Abschnitt des zweiten Individuums zusammengesetzt, ebenso der 2. Abschnitt des ersten Individuums mit dem 1. Abschnitt des zweiten Individuums:

Aus

 
 '1011110|010'   
 '0000110|000'
 

werden

 '1011110|000' 
 '0000110|010' 
 

Zur Lösung von Optimierungsmodellen ist es manchmal sinnvoll, diesen Vorgang mit nur einer bestimmten Wahrscheinlichkeit, der Kreuzungswahrscheinlichkeit stattfinden zu lassen und ansonsten die beiden Elternindividuen zunächst einmal unverändert zu übernehmen.

Mutation

Nun bleibt noch, die Mutation, also die zufällige Veränderung der neu entstandenen Individuen bzw. ihrer Erbinformation zu modellieren.

Wir realisieren Mutation, indem eine Position in der 0-1-Zeichenkette per Zufall ausgewählt und abgeändert wird.

Aus

 
'1011110|0|10'

wird

'1011110|1|10' 

Diesen Vorgang führen wir nur ab und zu (mit einer bestimmten Mutationswahrscheinlichkeit) bei einem neu generierten Individuum aus.

Algorithmus

Das gesamte Verfahren lässt sich mit dem folgenden Algorithmus beschreiben.

ALGORITHMUS loesung mit genetischem Algorithmus  
erzeuge eine initiale Population 
SOLANGE das Abbruchkriterium nicht erfüllt ist: 
	lege eine neue Population an 
	SOLANGE die Populationsgröße nicht erreicht ist: 
		wähle durch Selektion 2 Individuen aus
		erzeuge 2 neue Individuen durch Kreuzung der Individuen 
		verändere die Erbinformation der neuen Individuen durch Mutation 
		nimm die neuen Individuen in die neue Population auf 
		ersetze die alte durch die neue Population 
	bestimme das Individuum mit maximaler Fitness 

Beachte, dass der Algorithmus keinen Bezug auf das Rucksackproblem nimmt. Er kann also auch bei anderen Optimierungsproblemen benutzt werden, sofern geeignete Realisierungen der Modellierung der Erbinformation, der Selektion, der Kreuzung und der Mutation gefunden werden.