Einstieg in Künstliche Neuronen und ihre Trennlinie
Vom künstlichen Neuron zur Trennlinie
Wann ein künstliches Neuron feuert und wann nicht, kann mit Hilfe einer Trennlinie dargestellt werden.
Betrachte z.B. einmal das folgende künstliche Neuron:
Aufgabe 1: Neuron analysieren
Wie würde sich das künstliche Neuron verhalten, wenn wir als Eingänge nur die Werte 0 und 1 zulassen würden?
Fülle die Wahrheitstabelle unten korrekt aus - zur Kontrolle erhältst du einen Haken, wenn dein Ergebnis stimmt.
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Die Eingänge eines künstlichen Neurons können aber nicht nur 0 und 1 sein, sondern beliebige (nicht-negative) Werte erhalten.
Aufgabe 2: Neuron analysieren - Teil 2
Bei welchen Werten für x2 würde das künstliche Neuron oben feuern, wenn x1=0.25 gelten würde?
Antwort: x2 kann alle Werten annehmen, die
Mit Hilfe einer Wertetabelle lässt sich das Verhalten eines künstlichen Neurons also nicht mehr beschreiben, da wir nicht nur vier Wertepaare sondern unendlich viele Wertepaare haben.
Die Wertepaare lassen sich als Punkte im Koordinatensystem darstellen.
Dazu werden die x1-Werte auf der x-Achse (der horizontalen Achse) dargestellt und die x2-Werte werden auf der y-Achse (der vertikalen Achse) dargestellt.
Bei einem Teil dieser Punkte wird das künstliche Neuron nun feuern. Bei den restlichen Punkten wird das Neuron nicht feuern.
Um die Punkte, bei denen das Neuron feuert, von denen zu trennen, bei denen das Neuron nicht feuert, benötigen wir eine Trennlinie (oder auch Separationsgerade).
Mathematisch betrachtet, lässt sich eine solche Trennlinie mit Hilfe einer linearen Gleichung beschreiben. Alle Punkte, bei denen das Neuron feuert, müssen sich dann mit einer lineare Ungleichung beschreiben lassen.
Aufgabe 3: Ungleichung finden
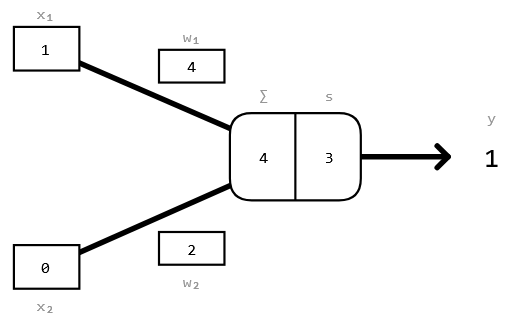
Rechts findest du noch einmal eine Darstellung des Neurons oben.
Beschreibe mit Hilfe einer mathematischen Ungleichung, bei welchen Wertepaaren das Neuron „feuert“.
Denke erst nach, dann findest du hier .
Das Neuron „feuert“ im Allgemeinen, wenn folgende Ungleichung erfüllt ist:
$x_1 \cdot w_1 + x_2 \cdot w_2 > s$
Daraus ergibt sich für unser Neuron in dieser Aufgabe:
$x_1 \cdot 4 + x_2 \cdot 2 > 3$
Aufgabe 4: Ungleichung nach x2 auflösen
Wir wollen die Ungleichung im Koordinatensystem darstellen.
Löse deshalb die Ungleichung aus der vorherigen Aufgabe nach x2 auf und nenne die Gleichung der linearen Funktion (mit x- und y-Notation), die die Trennlinie beschreibt.
Denke erst nach, dann findest du hier .
Die Ungleichung lautet $x_2 > -2 \cdot x_1 + 1,5$
Die Trennlinie hat somit die Gleichung $y=-2x+1,5$
Aufgabe 5: Darstellung der Trennlinie
In der graphischen Darstellung findest du schon einmal zwei grüne Punkte, in denen das Neuron feuern soll und zwei rote Punkte, in denen das Neuron nicht feuern soll.
- Stelle nun die Ungleichung aus der letzten Aufgabe (in x-y-Notation) hier dar, um alle (unendlich vielen) Wertepaare zu markieren, bei denen das Neuron feuert.
Klicke dazu in das Feld hinter dem "+" und mache deine Eingabe. - Gib in einem weiteren Feld ein: x=0.25
Dadurch werden alle Punkte markiert, bei denen wie in Aufgabe 2 gilt: x1=0.25
Vergleiche deine Lösung von Aufgabe 2 mit der Darstellung hier.

