Magische Tafeln
Ist das Zauberei?
Denke dir eine Zahl zwischen 0 und 63 aus. Klicke alle Tafeln an, auf der deine Zahl zu sehen ist und danach auf OK.
Wird deine Zahl durch Magie erraten?
Nein - es ist keine Zauberei!
Diesen einfachen Trick kannst du selbst mit den Karten nachmachen:
- Lasse jemand eine Zahl zwischen 0 und 63 auswählen.
- Er oder sie zeigt dir anschließend, auf welchen Karten diese Zahl steht.
- Addiere von jeder gezeigten Karte die erste Zahl (1, 2, 4, 8, 16 oder 32).
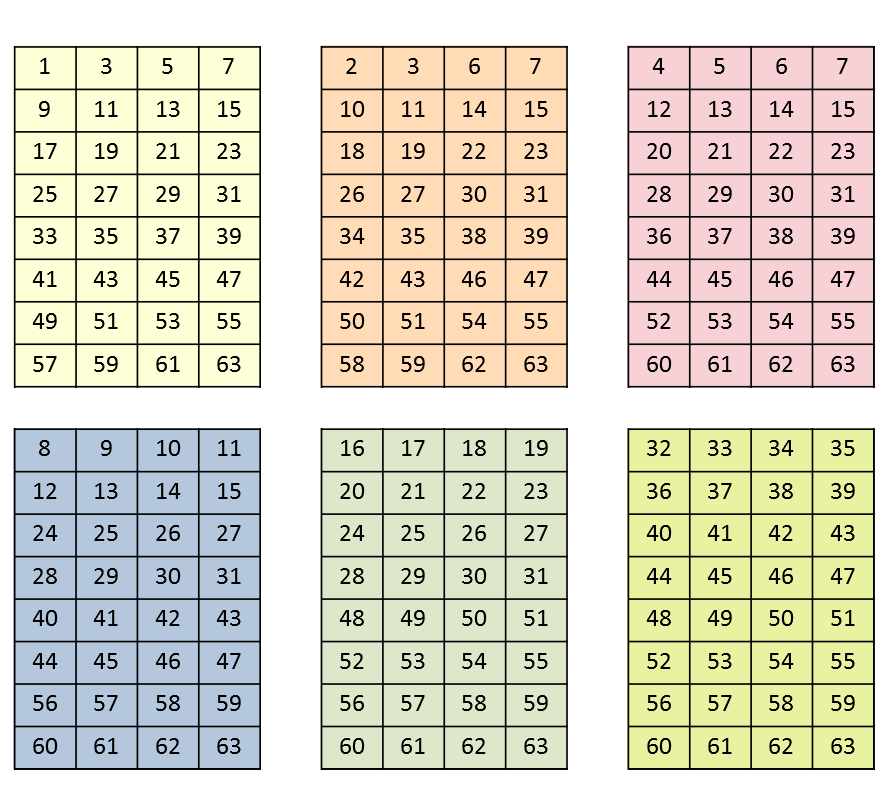
25 steht auf der Karte mit der 1 links oben, mit der 8 links oben und der 16 links oben.
1 + 8 + 16 = 25.
Aufgabe 1
Geht in Zweiergruppen zusammen und erratet gegenseitig eure Zahlen. Analysiert dabei die einzelnen Karten. Sammelt Regelmäßigkeiten oder Auffälligkeiten. Könnt ihr diese Erkenntnisse mit dem Binärsystem in Verbindung bringen?
Wie funktioniert der Trick? Hier die Erklärung:
Jede Karte enthält Zahlen nach einem ganz bestimmten Schema:
- Die erste Karte mit der 1 links oben enthält alle Zahlen, die umgerechnet als Binärzahl bei der Stelle mit Wertigkeit 1 eine 1 haben:
1 (=1), 3 (=11), 5 (=101), 7(=111), u.s.w. - Die zweite Karte mit der 2 links oben enthält alle Zahlen, die umgerechnet als Binärzahl bei der Stelle mit Wertigkeit 2 eine 1 haben:
2 (=10), 3 (=11), 6 (=110), 7(=111), u.s.w. - Die dritte Karte mit der 4 links oben enthält alle Zahlen, die umgerechnet als Binärzahl bei der Stelle mit Wertigkeit 4 eine 1 haben:
4 (=100), 5 (=101), 6 (=110), 7(=111), u.s.w. - Die vierte Karte mit der 8 links oben enthält alle Zahlen, die umgerechnet als Binärzahl bei der Stelle mit Wertigkeit 8 eine 1 haben:
8 (=1000), 9 (=1001), 10 (=1010), 11(=1011), u.s.w. - Die fünfte Karte mit der 16 links oben enthält alle Zahlen, die umgerechnet als Binärzahl bei der Stelle mit Wertigkeit 16 eine 1 haben:
16 (=10000), 17 (=10001), 18 (=10010), 19(=10011), u.s.w. - Die sechste Karte mit der 32 links oben enthält alle Zahlen, die umgerechnet als Binärzahl bei der Stelle mit Wertigkeit 32 eine 1 haben:
32 (=100000), 33 (=100001), 34 (=100010), 35(=100011), u.s.w.
Jede Karte entspricht bei einer Binärzahl also genau einer Stelle (mit der Wertigkeit links oben 1, 2, 4, 8, 16 oder 32).
Das heißt, man fragt mit jeder Karte ab, ob die Stelle mit ihrer Wertigkeit einer 1 oder 0 entspricht --> einer 1, wenn die zahl darauf vorkommt und einer 0, wenn sie nicht dabei vorkommt.
| Zahl | Binärzahl |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| ... | ... |
