Station - Erzeugung der Schlüssel

Ein Blick in CrypTool

Das Software-Werkzeug CrypTool zeigt, wie Schlüssel erzeugt werden.

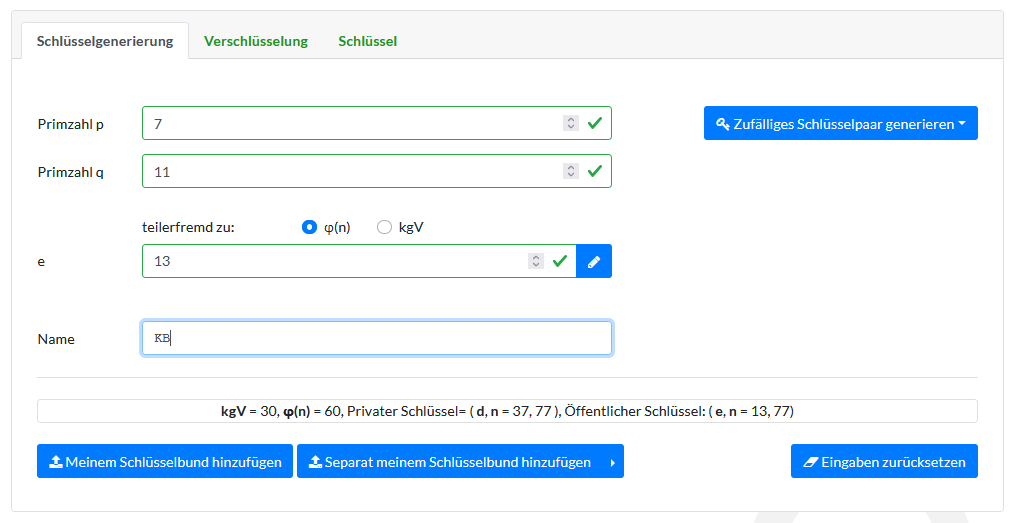
Schritt 1: Primzahlen als Ausgangspunkt

Zunächst werden zwei verschiedene Primzahlen p und q gewählt. Im Beispiel sind es p = 7 und q = 11.

Bei realen Anwendungen arbeitet man mit großen Primzahlen. Warum man große Primzahlen benötigt wird im Abschnitt Station - Sicherheit des Verfahrens geklärt.

Schritt 2: Konstruktion des öffentlichen Schlüssels

Aus den beiden Primzahlen p und q berechnet man die Zahlen n = p * q und φ(n) = (p-1) * (q-1). Im vorliegenden Beispiel erhält man n = 77 und φ(n) = 60

Für den öffentlichen Schlüssel wählt man jetzt eine Zahl e mit 1 < e < φ(n), die keine gemeinsamen Teiler mit φ(n) hat. Im Beispiel wurde die Zahl e = 13 gewählt.

Der öffentliche Schlüssel ist dann das Zahlenpaar (e, n). Im Beispiel erhält man das Zahlenpaar (13, 77).

Schritt 3: Konstruktion des privaten Schlüssels

Für den privaten Schlüssel benötigt man eine Zahl d mit [e*d]%φ(n) = 1. Die Zahl d ist also das modulare Inverse von e bzgl. des Moduls φ(n). Im vorliegenden Beispiel erhält man d = 37.

Der private Schlüssel ist das Zahlenpaar (d, n). Im Beispiel erhält man das Zahlenpaar (37, 77).

Bemerkung

Das ist alles ziemlich kompliziert und zunächst undurchschaubar. Die folgenden Abschnitte sollen hier etwas Klarheit schaffen.

Aufgabe 1

Du kannst das Schlüsselpaar testen, indem du einen kurzen Text mit den erzeugten Schlüsseln ver- und entschlüsselst. Lade hierzu die Datei chiffriersystemModularePotenz.py herunter. Mit den vorgegebenen Funktionen kannst du jetzt das RSA-Verfahren durchspielen, z.B. indem du das folgende Testprogramm mit deinen Schlüsseln ausführst.

from chiffriersystemModularePotenz import *
# Schluesseltest
print("Test")
abc = ' ABCDEFGHIJKLMNOPQRSTUVWXYZ'
block = 1
p = 7
q = 11
n = p*q
e = 13
d = 37
oeffentlicherSchluessel = (e, n)
privaterSchluessel = (d, n)
quelltext = 'ASTERIX'
quellcode = codierung(quelltext, block, abc)
geheimcode = verschluesselung(quellcode, oeffentlicherSchluessel)
entschluesseltercode = verschluesselung(geheimcode, privaterSchluessel)
entschluesseltertext = decodierung(entschluesseltercode, block, abc)
print("Quelltext: ", quelltext)
print("Quellcode: ", quellcode)
print("Geheimcode: ", geheimcode)
print("Entschluesselter Code: ", entschluesseltercode)
print("Entschluesselter Text: ", entschluesseltertext)