Aufsammeln von Wegknoten

Aufsammeln in einer Liste

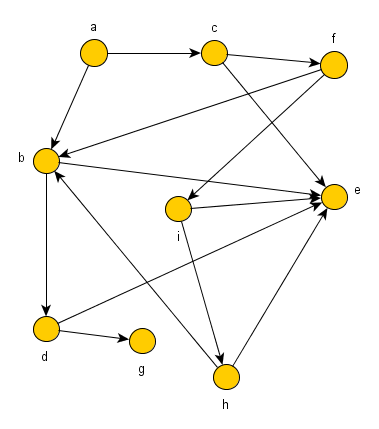
Wir betrachten weiterhin die Wegsuche in gerichteten Graphen ohne Kreise und verdeutlichen die Ergebnisse am folgenden Beispielgraphen.

Die folgenden Regeln zur Festlegung eines weg0-Prädikats benutzen eine Liste, um Knoten entlang eines Weges aufzusammeln.

% Graph
kante(a, b).
kante(a, c).
kante(b, d).
kante(b, e).
kante(c, e).
kante(c, f).
kante(d, g).
kante(d, e).
kante(f, b).
kante(f, i).
kante(h, e).
kante(h, b).
kante(i, e).
kante(i, h).
% Weg
weg0(X, X, []).
weg0(X, Y, [Z|W]) :- kante(X, Z), weg0(Z, Y, W).

Die "Logik" der beiden Regeln zur Festlegung des weg0-Prädikats kann so in Worten beschrieben werden:

Regel 1: weg0(X, X, []).
Die leere Liste [] enthält die Wegknoten eines Weges von X nach X (ohne das X).
Regel 2: weg0(X, Y, [Z|W]) :- kante(X, Z), weg0(Z, Y, W).
Die Liste [Z|W] enthält die Wegknoten eines Weges von X nach Y (ohne das X),
  wenn es eine Kante von X nach Z gibt und
  wenn die Liste W die Wegknoten eines Weges von Z nach Y (ohne das Z) enthält.

Aufgabe 1

Teste das weg0-Prädikat mit geeigneten Anfragen.

?- weg0(a, b, W).
...

Aufgabe 2

Was leistet das folgendermaßen festgelegte weg-Prädikat?

% Weg
weg0(X, X, []).
weg0(X, Y, [Z|W]) :- kante(X, Z), weg0(Z, Y, W).
weg(X, Y, [X|W]) :- weg0(X, Y, W).

Teste es mit geeigneten Anfragen. Erkläre das Verhalten.