inf-schule | Einzelne Neuronen - Trennlinie

Trennlinien bestimmen

Vom künstlichen Neuron zur Trennlinie

Betrachte z.B. einmal das folgende künstliche Neuron:

Aufgabe 1: Neuron analysieren

Wie würde sich das künstliche Neuron verhalten, wenn wir als Eingänge nur die Werte 0 und 1 zulassen würden?
Fülle die Wahrheitstabelle unten korrekt aus - zur Kontrolle erhältst du einen Haken, wenn dein Ergebnis stimmt.

x₁	x₂	y
0	0
0	1
1	0
1	1

Eingangsraum

Die Tabelle im obigen Beispiel zeigt die Ergebnisse für die Eingangskombinationen $(0,0)$, $(0,1)$, $(1,0)$ und $(1,1)$ die jeweiligen Ausgangswerte. Grundsätzlich könnten die Eingänge $x_1$ und $x_2$ aber auch alle möglichen anderen Werte annehmen. Aus dem Mathematikunterricht weiß man: Man kann solche Werte-Paare nicht nur in einer Wertetabelle, sondern auch in einem Koordinatensystem darstellen, wenn man z.B. $x_1$ auf der Rechtsachse ($x$-Achse) abträgt und $x_2$ auf der Hochachse ($y$-Achse) abträgt.
Dies machen wir für sehr viele (zufällige) Punkte und färben sie gelb, wenn das Neuron feuert.
Die vier Eingangskombinationen aus der Tabelle zeichnen wir ebenfalls ein (als große Punkte). Diese liegen genau in den Ecken eines Quadrats.
Die $x_1 / x_2$-Ebene, also letztlich unser Koordinatensystem, wird auch als "Eingangsraum" des Neurons bezeichnet, weil jeder Punkt darin einer bestimmten Kombination der Eingänge entspricht.

Das Neuron und seine Trennlinie im Eingangsraum

In der Abbildung sieht man, dass die Eingangswert-Paare, für die das Neuron feuert, eher rechts oben liegen, während die Eingangswert-Paare, für die das Neuron nicht feuert, eher links unten liegen.
Da stellt sich natürlich die Frage: Kann man eine Grenzlinie ziehen, die die gelben von den schwarzen Punkten trennt? Und welche Form hat diese Grenzlinie? Probiert man es aus, so stellt man fest: Man kann nicht nur irgendeine Grenzlinie finden, sondern sogar immer auch eine Gerade, also eine Grenzlinie, die besonders einfach mit einem Lineal konstruiert werden kann.

Aufgabe 2: Trennlinie mathematisch beschreiben

Statt sie mit dem Lineal zu ziehen, versuchen wir hier, die Trennlinie durch eine mathematische Gleichung zu finden. Diese Gleichung kannst Du im folgenden Geogebra-Plugin eingeben. Tipp: Die Gleichung ist ganz einfach. Sie hat die Form $$zahl_1 * x + zahl_2 * y = zahl_3 $$ Ein weiterer Tipp: Die drei Zahlen haben sehr viel mit den Werten $w_1$, $w_2$ und $s$ des Neurons zu tun.

Die Gleichung für unsere Trennlinie lautet $$2 * x + 1 *y = 1.5$$ wobei die 2 gerade der Wert von Gewicht $w_1$ war, die 1 der Wert von Gewicht $w_2$ und die 1.5 der Wert des Schwellenwerts $s$.

Zusammenhang zwischen Trennlinie und synaptischen Gewichten

Allgemein kann man zeigen, dass die Trennlinie bei einem Neuron mit den Gewichten $w_1$, $w_2$ und Schwellenwert $s$ immer durch die Gleichung $$w_1 \cdot x_1 + w_2 \cdot y_2 = s$$ beschrieben werden kann.

Das ist sehr praktisch: Künftig müssen wir also gar nicht mehr hunderte von Punkten ausprobieren, um die verschiedenen Bereiche des Eingangsraum zu finden. Man kann direkt aus den Gewichten und dem Schwellenwert die Lage der Trenngerade ablesen.

Aufgabe 3: Ungleichung statt Gleichung

Ändere in dem Geogebra-Plugin oben die Gleichung so ab, dass eine Ungleichung daraus wird, also $$2*x + 1*y > 1.5$$ Beschreibe, was sich an der Darstellung ändert und welchen Vorteil dies haben könnte, wenn man bestimmen möchte, für welche Eingaben ein Neuron feuert und für welche nicht?

Aufgabe 3: Ungleichung finden

a) Bestimme Trenngerade mit Hilfe einer Ungleichung in Geogebra.

b) Fülle mit Hilfe des Ergebnisses direkt die Wahrheitstabelle aus.

x₁	x₂	y
0	0
0	1
1	0
1	1

Trennlinien und Einteilung von Gegenständen mit Eigenschaften

Worum geht es nun bei einem solchen künstlichen Neuron und der Trennlinie?

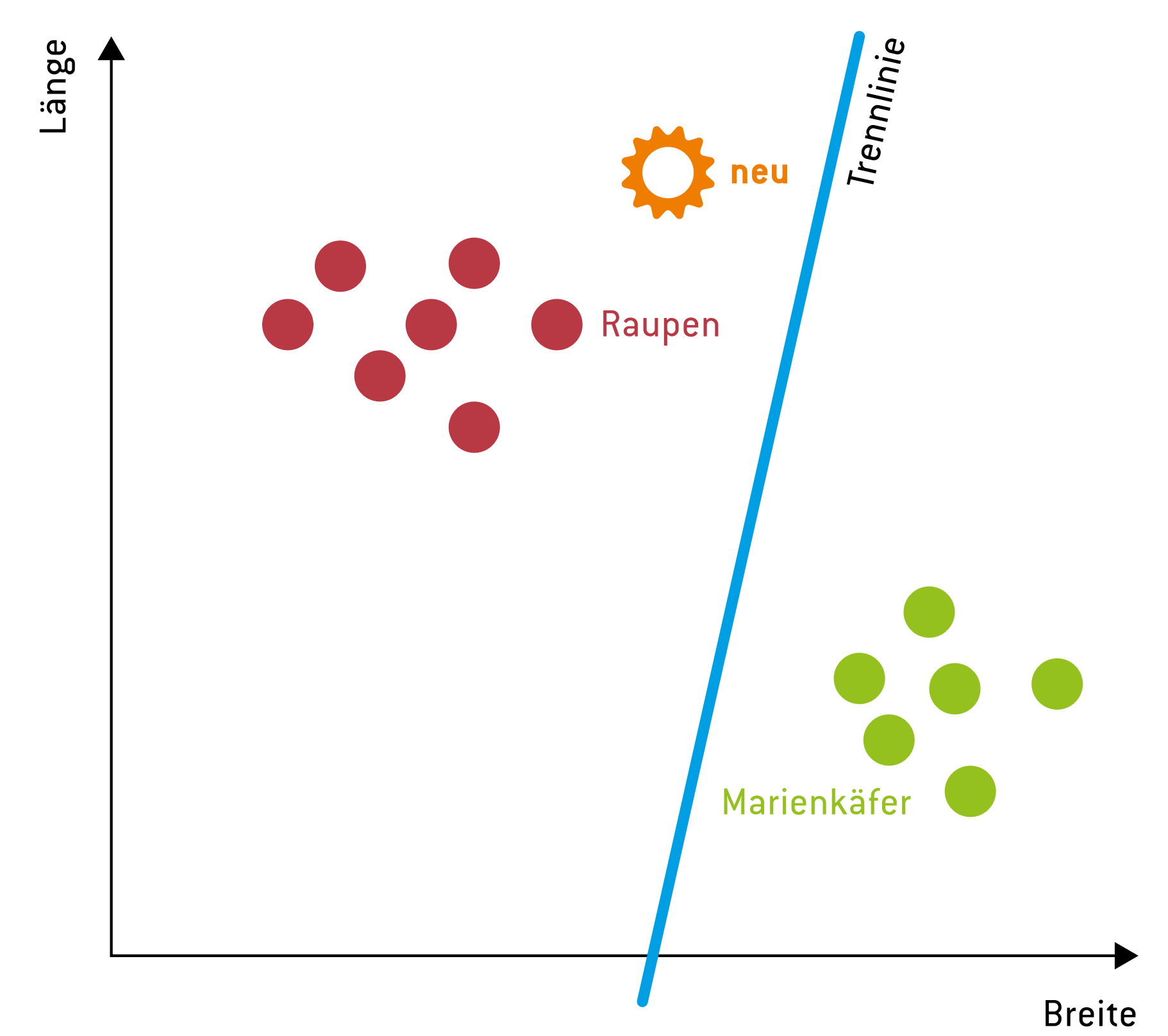
Nehmen wir der Einfachheit halber an, das Neuron hätte aufgrund von Länge und Breite der Tiere eine Trennlinie zwischen Raupen und Marienkäfern gefunden. Dann könnten ab jetzt auch bisher unbekannte Tiere in die Klasse „Raupe” bzw. „Marienkäfer” eingeteilt werden.

Die Schwierigkeit besteht darin, die passenden Gewichte von Hand zu bestimmen.

Es gibt jedoch Verfahren, mit denen sich ein Neuron trainieren lässt - wir sprechen dann von einem selbst lernenden Neuron.