Algorithmen zur Turnierplanung

Ein Turnier mit n Teilnehmern

Wir betrachten jetzt verallgemeinernd Turniere mit n Teilnehmern, wobei n eine gerade natürliche Zahl sein soll. Die Teilnehmer werden von 0 an durchnummeriert: 0, 1, 2, ..., n-1.

Hier als Beispiel ein fertiger Turnierplan für n = 8:

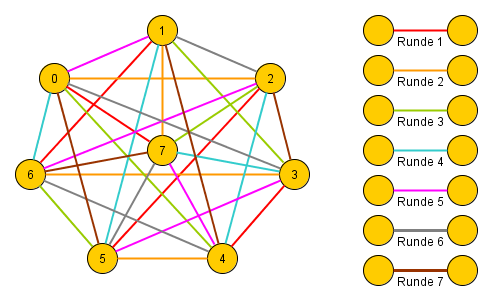
Eine informelle Verfahrensbeschreibung

Die Erzeugung solcher Turnierpläne soll so beschrieben werden, dass man sie - ohne viel Nachdenken - direkt erstellen kann. Hier ein Vorschlag:

# Erzeugung eines Turnierplans mit n Teilnehmern
Ordne die Teilnehmer 0, 1, ..., (n-2) zu einem (n-1)-Eck an.
Setze den Teilnehmer n-1 in die Mitte des (n-1)-Ecks.
# Runde 1
Verbinde n-1 mit 0.
Verbinde die Ecken des (n-1)-Ecks, die von 0 aus in 1 Schritt erreichbar sind.
Verbinde die Ecken des (n-1)-Ecks, die von 0 aus in 2 Schritten erreichbar sind.
...
Verbinde die Ecken des (n-1)-Ecks, die von 0 aus in n/2-1 Schritten erreichbar sind.
# Runde 2
Verbinde n-1 mit 1.
Verbinde die Ecken des (n-1)-Ecks, die von 1 aus in 1 Schritt erreichbar sind.
Verbinde die Ecken des (n-1)-Ecks, die von 1 aus in 2 Schritten erreichbar sind.
...
Verbinde die Ecken des (n-1)-Ecks, die von 1 aus in n/2-1 Schritten erreichbar sind.
# Runde 3
Verbinde n-1 mit 2.
Verbinde die Ecken des (n-1)-Ecks, die von 2 aus in 1 Schritt erreichbar sind.
Verbinde die Ecken des (n-1)-Ecks, die von 2 aus in 2 Schritten erreichbar sind.
...
Verbinde die Ecken des (n-1)-Ecks, die von 2 aus in n/2-1 Schritten erreichbar sind.
# ...
...

Aufgabe 1

(a) Analysiere den Vorschlag: Was muss ein Turnierplaner wissen und verstehen, um nach der gegebenen Verfahrensbeschreibung einen Turnierplan erstellen zu können?

(b) Du kannst die Verfahrensbeschreibung auch mit Freunden oder Bekannten ausprobieren, die sich bisher noch nicht mit Turnierplanung beschäftigt haben. Lege ihnen die Beschreibung vor und schaue, inwieweit sie mit der Beschreibung klarkommen.

(c) Könnte man die Verfahrensbeschreibung auch an einen Computer übergeben? Welche Möglichkeiten und Schwierigkeiten vermutest du?

Eine präzisere Verfahrensbeschreibung

Ziel der folgenden Überlegungen ist es, die Verfahrensbeschreibung weiter zu präzisieren, so dass sie schließlich von einem Computer ausgeführt werden kann.

Wir betrachten weiterhin Turniere mit n Teilnehmern, wobei n eine gerade natürliche Zahl sein soll. Die Teilnehmer werden von 0 an durchnummeriert: 0, 1, 2, ..., n-1.

Die Spielpaare der jeweiligen Spielrunden kann man auch so bestimmen:

Runde 1:
7     0-1+7  0-2+7  0-3+7
|      |      |      |
0     0+1    0+2    0+3

Runde 2:
7     1-1    1-2+7  1-3+7
|      |      |      |
1     1+1    1+2    1+3

Runde 3:
7     2-1    2-2    2-3+7
|      |      |      |
2     2+1    2+2    2+3

Runde 4:



Runde 5:



Runde 6:
7     5-1    5-2    5-3
|      |      |      |
5     5+1    5+2-7  5+3-7

Runde 7:

Aufgabe 2

(a) Analysiere das Verfahren. Welche Muster kannst du erkennen? Ergänze die noch fehlenden Runden.

(b) Erläutere die folgende Verfahrensbeschreibung anhand der oben gezeigten "Berechnungen" für die einzelnen Spielrunden.

# Erzeugung eines Turnierplans mit 8 Teilnehmern
Für i von 0 bis 6:
    # Runde i+1
    Ausgabe des Spielpaars: 7:i
    Für j von 1 bis 3:
        Setze a auf i-j.
        Setze b auf i+j.
        Wenn a < 0:
            Erhöhe a um 7.
        Wenn b > 6:
            Verringere b um 7.
        Ausgabe des Spielpaars: a:b

(c) Wie müsste man die Verfahrensbeschreibung abändern, damit sie für n Teilnehmer funktioniert?

Eine computergerechte Verfahrensbeschreibung

Damit ein Computer das beschriebene Verfahren automatisiert durchführen kann, muss man es ihm in einer computergerechten Form übergeben. Hier eine solche Beschreibung mit Hilfe der Programmiersprache Python.

# Erzeugung eines Turnierplans mit n Teilnehmern
# Eingabe von n
n = int(input('Anzahl der Teilnehmer: '))
# Erzeugung und Ausgabe der Spielpaarungen
i = 0
while i < n-1:
    print('Runde ' + str(i+1) + ':')
    print(n-1, ':', i)
    j = 1
    while j < n/2:
        a = i-j
        b = i+j
        if a < 0:
            a = a + (n-1)
        if b > n-2:
            b = b - (n-1)
        print(a, ':', b)
        j = j+1
    i = i+1

Wenn man das Programm ausführt, dann erhält man für die Eingabe 8 die folgenden Ausgaben.

>>> 
Anzahl der Teilnehmer: 8
Runde 1:
7 : 0
6 : 1
5 : 2
4 : 3
Runde 2:
7 : 1
0 : 2
6 : 3
5 : 4
Runde 3:
7 : 2
1 : 3
0 : 4
6 : 5
Runde 4:
7 : 3
2 : 4
1 : 5
0 : 6
Runde 5:
7 : 4
3 : 5
2 : 6
1 : 0
Runde 6:
7 : 5
4 : 6
3 : 0
2 : 1
Runde 7:
7 : 6
5 : 0
4 : 1
3 : 2

Aufgabe 3

(a) Überprüfe, ob der erzeugte Turnierplan mit den oben ermittelten Spielrunden übereinstimmt.

(b) Teste selbst das Programm für verschiedene Eingaben.