Strukturierung: Reduktion von Ausdrücken

Reduktion von Ausdrücken

Die von uns zur Programmierung genutzten Ausdrücke werden in Racket schrittweise ausgewertet, bis ein Ausdruck erreicht wird, der nicht weiter ausgewertet werden kann, zum Beispiel das Endergebnis einer mathematischen Rechnung.

Reduktionsregeln umfassen beispielsweise die Reihenfolge, in der Teilausdrücke ausgewertet werden, sowie die Art und Weise, wie Parameter einer Funktion durch die entsprechenden Übergabedaten ersetzt werden.

Aufgabe 1: Unterschiedliche Auswertungsreihenfolgen

(a) Analysiere den folgenden Ausdruck und stelle sicher, dass du verstehst, welche Funktionalität dieser erfüllt. Führe anschließend den Stepper für den Ausdruck aus.

((lambda (a b) (* 2 (+ a b)))
 (+ 1 1) (/ 6 2) )

Wie du in Aufgabenteil (a) gesehen hast, wertet Racket die beiden Ausdrücke (+ 1 1) und (/ 6 2) aus, bevor diese an die Funktion übergeben werden. Diese Reihenfolge stellt jedoch nicht die einzige mögliche Auswertungsreihenfolge dar.

(b) Die untere Tabelle zeigt dir zwei verschiedene Möglichkeiten den Ausdruck aus Aufgabenteil (a) auszuwerten. Vergleiche die beiden Auswertungsreihenfolgen und beschreibe die Strategie der verzögerten Auswertung.

Schritt	Direkte Auswertung	Verzögerte Auswertung
0	((lambda (a b) (* 2 (+ a b))) (+ 1 4) (/ 6 2) )	((lambda (a b) (* 2 (+ a b))) (+ 1 4) (/ 6 2) )
1	((lambda (a b) (* 2 (+ a b))) 5 (/ 6 2) )	(* 2 (+ (+ 1 4) (/ 6 2)))
2	((lambda (a b) (* 2 (+ a b))) 5 3)	(* 2 (+ 5 (/ 6 2)))
3	(* 2 (+ 5 3))	(* 2 (+ 5 3))
4	(* 2 8)	(* 2 8)
5	16	16

(c) Untenstehend findest du zwei Ausdrücke, lege für diese analog zu Aufgabenteil (b) je eine Tabelle zum Vergleich der beiden Auswertungsstrategien an.

;Ausdruck 1
((lambda (a b) (+ (* a a) (* b b)))
 (+ 1 1) (/ 6 2) )

;Ausdruck 2    
((lambda (a b c) (if a b c))
 #t 0 (* 4 (- 1 3)) )

Hinweis: Der Ausdruck (if #t ausdruck-a ausdruck-b) wertet zu ausdruck-a aus.

(d) Beantworte anhand deiner beiden Tabellen aus Aufgabenteil (c) die folgenden Fragen:

1. Unterscheiden sich die Ergebnisse der Ausdrücke für die beiden Strategien?
2. Welche Strategie ist für Ausdruck 1 effizienter?
3. Welche Strategie ist für Ausdruck 2 effizienter?

Eager und Lazy Evaluation

Um Ausdrücke mit Funktionsaufrufen auszuwerten, gibt es zwei gängige Möglichkeiten:

Zum einen können die Ausdrücke, die die Übergabedaten darstellen, direkt ausgewertet und anschließend an die Funktion übergeben werden. Bei dieser direkten Auswertungsstrategie spricht man meist von eifriger Auswertung bzw. in der gebräuchlicheren englischen Terminologie von Eager Evaluation. Die Nutzung von Eager Evaluation kann beispielsweise in Fallunterscheidungen jedoch dazu führen, dass Ausdrücke ausgewertet werden, die überhaupt nicht benötigt werden, da der Fall des Ausdrucks nicht eintrifft.

Zum anderen können die Ausdrücke, die die Übergabedaten darstellen, auch unausgewertet an die Funktion übergeben werden und entsprechend als unausgewertete Ausdrücke in den Funktionskörper eingefügt werden. Durch diese verzögerte Auswertung werden die Ausdrücke erst dann ausgewertet, wenn sie tatsächlich benötigt werden. Diese Strategie kann allerdings dazu führen, dass dieselben Ausdrücke mehrfach vorkommen. Die meisten Sprachen, die eine verzögerte Auswertung benutzen, nutzen daher zusätzlich Memoisation.

Memoisation bedeutet nichts anderes, als dass die Ergebnisse ausgewerteter Ausdrücke zwischengespeichert werden, wodurch dieselben Ausdrücke nicht mehr mehrfach ausgewertet werden müssen. Bei einer verzögerten Auswertung, die Memoisation unterstützt, spricht man auch von fauler Auswertung bzw. in der gebräuchlicheren englischen Terminologie von Lazy Evaluation.

Schritt	Verzögerte Auswertung - ohne Memoisation	Lazy Evaluation
0	((lambda (a) (* a a a)) (- 5 3))	((lambda (a) (* a a a)) (- 5 3))
1	(* (- 5 3) (- 5 3) (- 5 3))	(* (- 5 3) (- 5 3) (- 5 3))
2	(* 2 (- 5 3) (- 5 3))	(* 2 2 2)
3	(* 2 2 (- 5 3))	8
4	(* 2 2 2)
5	8

Aufgabe 2: Exkurs: Lazy Evaluation für unendliche Datenstrukturen

Die Nutzung von Lazy Evaluation bietet zudem eine besondere Möglichkeit: die Bildung und Verarbeitung von unendlichen Datenstrukturen.

Eine solche unendliche Struktur wäre beispielsweise die Fibonacci-Folge. Diese stellt eine Zahlenreihe dar, bei der jede Zahl die Summe der zwei vorherigen ist. Die ersten beiden Zahlen sind mit 0 und 1 fest definiert:

• die erste Zahl ist 0
• die zweite Zahl ist 1
• die dritte Zahl ist die Summe der ersten und zweiten Zahl: 0 + 1 = 1
• die vierte Zahl ist die Summe der zweiten und dritten Zahl: 1 + 1 = 2
• usw.

Eine theoretische Definition der Fibonacci-Folge in Racket ist die folgende:

(define naechste-fibonacci-zahl
  (lambda (a b)
    (cons a (naechste-fibonacci-zahl b (+ a b)))))

(define fibonacci-folge
  (naechste-fibonacci-zahl 0 1))

Mit der Definition fibonacci-folge wird dabei theoretisch die gesamte unendliche Folge der Fibonacci-Zahlen definiert. Durch Aufruf der Funktion naechste-fibonacci-zahl mit den ersten beiden Fibonacci-Zahlen 0 und 1 erzeugt die Funktion naechste-fibonacci-zahl rekursiv eine unendliche Liste.

(a) Analysiere die obigen Definitionen und stelle sicher, dass du verstehst, welche Funktionalitäten diese erfüllen. Führe anschließend den Stepper aus und erkläre, warum der Ausdruck (naechste-fibonacci-zahl 0 1) nicht terminiert.

In einer Sprache, die Lazy Evaluation unterstützt, ist die obige Definition jedoch möglich, da die entstehende Liste bei Definition nicht vollständig erzeugt wird, sondern die einzelnen Elemente erst dann berechnet werden, wenn sie tatsächlich benötigt werden. Diese Eigenschaft können wir leicht testen, denn Racket bietet auch eine Version an, die Lazy Evaluation als Auswertungsstrategie nutzt.

(b) Ändere deine verwendete Racket-Version in DrRacket. Klicke hierzu in DrRacket unten links auf deine aktuelle Version und wähle den obersten Punkt "Die Sprache Racket" aus. Diese Auswahl erlaubt es dir im Definitionsfenster die genutzte Sprache festzulegen.

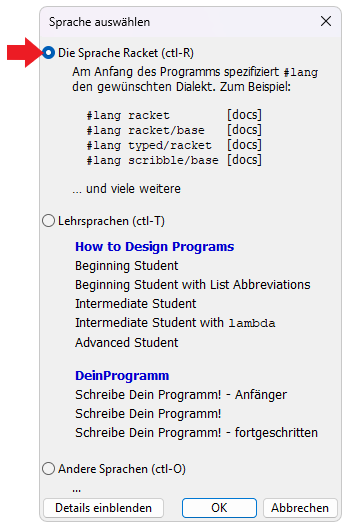
(c) Übertrage den unten stehenden Code in dein Definitionsfenster. Die oberste Zeile #lang lazy gibt an, dass wir die Racket-Version mit Lazy Evaluation nutzen.

#lang lazy

(define naechste-fibonacci-zahl
  (lambda (a b)
    (cons a (naechste-fibonacci-zahl b (+ a b)))))

(define fibonacci-folge
  (naechste-fibonacci-zahl 0 1))

Leider besitzt diese Racket-Version keinen Stepper, weswegen wir uns die schrittweise Auswertung nicht anzeigen lassen können. Dennoch können wir die Korrektheit der entstehenden Liste testen. Die drei unten stehenden Racket-Ausdrücke liefern dir das Element der Liste an den Positionen 0, 1 und 2:

(list-ref fibonacci-folge 0)
(list-ref fibonacci-folge 1)
(list-ref fibonacci-folge 2)

(d) Teste die Korrektheit der Definition fibonacci-folge mit geeigneten Ausdrücken in der REPL.