Mathematische Grundlagen

Um das Folgende ein wenig besser zu verstehen, benötigst du einige mathematische Grundlagen. Vieles ist dir vermutlich schon bekannt oder noch bekannt, aber es schadet nicht, wenn du noch einmal einen Überblick gewinnst.

3D-Koordinatensystem

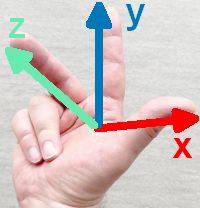
Wie schon beschrieben, haben wir durch eine dritte Achse ein dreidimensionales "rechtshändiges Koordinatensystem"

Aus der Mittelstufe kennst du bereits die Angabe eine Punktes im Koordinatensystem als Wertepaar - z.B. (3,5) für 3 Einheiten auf der x-Achse und 5 Einheiten auf der y-Achse. Man sagt dazu auch Tupel.

Nun wird aus den 2-Tupel durch Hinzufügen der z-Koordinate ein 3-Tupel.
So beschreibt der Code translate([10,-5,12]) cube(7); die Verschiebung des nachfolgenden Objekts (ein Würfel mit der Kantenlänge 7) um 10 Einheiten in x-Richtung und um 5 Einheiten in negativer y-Richtung und um 12 Einheiten in z-Richtung.
Man bezeichnet dabei [10,-5,12] als Vektor (du kennst den Begriff vermutlich schon aus der Geometrie oder aus der Physik).

Mehrere Objekte kombinieren

Tauchen mehrere Objekte in einer Darstellung auf, scheint das zunächst einmal kein Problem:

Diese Situation ist vergleichbar mit zwei Mengen in der Mathematik, die keine gemeinsamen Elemente haben (man sagt: Die Mengen sind disjunkt).

Doch was passiert, wenn die Objekte gemeinsame Punkte, bzw. die Mengen gemeinsame Elemente haben? Im Wesentlichen unterscheidet man folgende Situationen:

Aufgabe: Umsetzung in OpenSCAD

Die entsprechenden Funktionen in OpenSCAD lauten union(){...}, difference(){...} und intersection(){...}.

Wenn du in OpenSCAD mehrere Objekte beschreibst, dann wird implizit eine Vereinigung durchgeführt. Trotzdem kann es manchmal sinnvoll sein, "union" zu verwenden - z.B. wenn du innerhalb einer Differenz als "Subtrahend" eine Vereinigung festlegen möchtest.

Im folgenden siehst du einen Quelltext, der dir eine Übersicht über alle Kombinationsmöglichkeiten liefert. Lasse ihn dir in OpenSCAD darstellen, damit du die Objekte aus unterschiedlichen Perspektiven anschauen kannst.

// Die Objekte in getrennter Darstellung
translate([0,0,40])
union(){
    color("#0077b6")cube(size=10, center=true);
    translate([13,0,0])rotate([40,40,0])color("#fcca00")cylinder(18,2,2, center=true);
}

// Vereinigung
translate([0,0,20])
union(){
    color("#0077b6")cube(size=10, center=true);
    rotate([40,40,0])color("#fcca00")cylinder(18,2,2, center=true);
}

// Differenz
difference(){
    color("#0077b6")cube(size=10, center=true);
    rotate([40,40,0])color("#fcca00")cylinder(18,2,2, center=true);
}

// Schnittmenge
translate([0,0,-20])
intersection(){
    color("#0077b6")cube(size=10, center=true);
    rotate([40,40,0])color("#fcca00")cylinder(18,2,2, center=true);
}