Fehlererkennung

Grenzen des Übertragungsmediums

Die Übertragung von Daten ist nie ganz perfekt. Durch Grenzen technischer Systeme und äußere Einflüsse kann es immer vorkommen, dass Daten während des Transports verändert werden.

Ein Grundproblem der Datensicherung besteht darin, Fehler bei der Datenübertragung zwischen zwei Calliope mini zu erkennen und geeignete Maßnahmen zur Behandlung von Fehlern zu ergreifen.

Fehlererkennung mit einem Zusatzbit

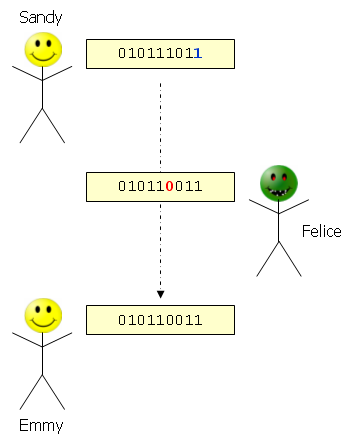
Sandy will Emmy eine Bitfolge senden. Felice, die für die Übertragung zuständig ist, ändert ab und zu ein Bit ab. Sandy und Emmy haben sich ein Verfahren ausgedacht, mit dem sie die Veränderung von Bits überprüfen wollen. Sandy zählt hierzu die Einsen in der zu übertragenen Bitfolge. Ist die Anzahl ungerade, so fügt Sandy der Bitfolge eine 1 hinzu, ansonsten eine 0.

Aufgabe 1

(a) Wie kann Emmy überprüfen, ob Felice ein Bit abgeändert hat? Funktioniert das auch, wenn Felice das Zusatzbit abändert?

(b) Kann Emmy feststellen, welches Bit abgeändert wurde?

(c) Felice ändert mehrere Bits ab. Welche Möglichkeiten ergeben sich für Emmy, solche Veränderungen zu erkennen?

(d) Du kannst das beschriebene Szenario auch mit dem Python-Programm fehlererkennungParitaet.py erkunden. Führe das Programm mehrfach aus und interpretiere die ausgegebenen Ergebnisse.

Aufgabe 2 - Erweiterter Sender und Empfänger

a) Passe den Sender und Empfänger für den Calliope mini aus Abschnitt ...3.5so an, dass mit Hilfe eines Paritätsbits Fehler erkannt werden. Im Fehlerfall soll eine entsprechende Meldung ausgegeben werden. Implementiere zuerst den Sender und teste ihn. Implementiere dann den Empfänger und teste das System.

b) Zum Testen kannst Du dieses Testprogramm verwenden, das einen einfachen Sender und Empfänger enthält. Im Sendemuster, das beim Drücken des Knopfes A gesendet wird ist jedoch ein Fehler im Paritätsbit eingebaut. Verbinde einen Calliope mini mit diesem Testprogramm mit dem Calliope mini, das dein Programm aus a) enthält und überprüfe, ob nach dem Senden des falschen Bitmusters eine Fehlermeldung auf dem von Dir programmierten Calliope mini angezeigt wird.

Aufgabe 3

Das Prüfverfahren wird jetzt verbessert. Diskutiere jeweils die möglichen Fehlerfälle und beurteile die Güte des Verfahrens.

(a) Prüfsummenverfahren: Gegeben ist eine Folge von Bytes (hier dezimal dargestellt) wie z.B. 72, 65, 78, 76, 79. Aus dieser Folge wird die Summe berechnet: 72 + 65 + 78 + 76 + 79 = 370. Damit das Ergebnis wieder ein Byte darstellt, bildet man anschließend den Rest bei der Division durch 256: 370 % 256 = 114. Versendet wird jetzt die erweiterte Nachricht 72, 65, 78, 76, 79, 114.

(b) Prüfrestverfahren: Gegeben ist eine Folge von 3 Bytes (hier dezimal dargestellt) wie z.B. 72, 65, 78. Aus dieser Folge von Zahlen wird eine 9-stellige Zahl gebildet: 072065078. Diese Zahl wird durch einen festen "geeigneten" Divisor geteilt: 72065078 % 171 = 35. Der Rest 35 wird jetzt als "Prüfzahl" benutzt und zusammen mit den Ausgangszahlen übertragen: 72, 65, 78, 35.

Fehlerbehandlung

Wurde ein Fehler erkannt, gibt es prinzipiell zwei Möglichkeiten wie man darauf reagieren kann: Man kann den Fehler ignorieren oder man kann versuchen ihn zu korrigieren. Tatsächlich gibt es beide Varianten in der Praxis.

Aufgabe 4

Bei Ethernet - einem der verbreitetsten Protokolle in der Praxis - werden fehlerhafte Pakete verworfen. Welche Vorteile hat das (Tipp: Schichten)? Wie könnte ein Verfahren aussehen, bei dem fehlerhafte Daten noch einmal gesendet werden?

Fehlerkorrektur

Die bisher benutzten Verfahren erlauben nur, das Vorhandensein von Fehlern zu erkennen. Man ist jedoch nicht in der Lage, Fehler genau lokalisieren und dann korrigieren zu können.

Aufgabe 5

In der folgenden Aufgabe soll ein einfaches Verfahren zur Fehlerkorrektur untersucht werden.

Gehe im Folgenden davon aus, dass nur 1 Bit abgeändert wird.

Eine Bitfolge wie z.B. '010111000' lässt sich auch folgendermaßen mit Zusatzbits anreichern:

010|1
111|1
000|0
---
101

Man schreibt die Bitfolge als zweidimensionales Muster in mehreren Zeilen auf. Dann bestimmt man für jede Zeile und jede Spalte ein Zusatzbit (z.B. mit dem Verfahren ganz oben). Aus dem erweiterten zweidimensionalen Bitmuster wird jetzt wieder nach einer vereinbarten Systematik eine Bitfolge erzeugt: '010111000110101'.

(a) Probiere das selbst aus und überlege dir, wie man eine Veränderung eines Bits jetzt genau lokalisieren kann.

(b) Worin liegen die Nachteile dieses Verfahrens?