Theorie - Kontextfreie Sprachen und Kellerautomaten
Von der kontextfreien Grammatik zum Kellerautomaten
Kellerautomaten sind in der Lage, Ableitungen mit einer kontextfreien Grammatik zu simulieren. Wir verdeutlichen diese Simulation anhand eines Beispiels.
Gegeben sei eine Grammatik G für die Sprache
Lab = {anbn | n = 1, 2, 3, ...}
der Klammerausdrücke:
S -> aSb S -> λ
Zur Grammatik G lässt sich der Kellerautomat KG konstruieren:
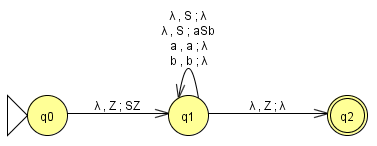
Beachte, dass alle Produktionen der Grammatik in den Zustandsübergängen des Kellerautomaten kodiert sind.
Der Kellerauromat ist so konstruiert, dass jede Ableitung mit Produktionen der Grammatik G
mit Hilfe von Zustandsübergängen des Kellerautomaten simuliert werden kann. Wir verdeutlichen dies
anhand der folgenden Ableitung des Worts aabb:
S -> aSb -> aaSbb -> aabb
Diese Ableitung lässt sich mit dem Kellerautomaten wie folgt nachbilden:
Der erste Zustandsübergang speichert das Startsymbol
S im Keller ab:
q0; Z aabb | λ,Z;SZ q1; SZ aabb
Der nächste Zustandsübergang simuliert einen Ersetzungsschritt mit der Produktion S -> aSb
im Keller. Hierzu wird das oberste Kellersymbol S entfernt und stattdessen die Symbolfolge
aSb abgespeichert. Im Keller befindet sich dann die Symbolfolge aSbZ.
q1; SZ aabb | λ,S;aSb q1; aSbZ aabb
Bevor der nächste Ersetzungsschritt mit einer Produktion der Grammatik simuliert werden kann, muss das Terminalsymbol ganz oben im Keller entfernt werden. Bei diesem Schritt wird dann auch das erste Symbol des Eingabeworts verarbeitet.
q1; aSbZ aabb | a,a;λ q1; SbZ abb
Analog werden jetzt die nächsten Schritte der Ableitung das Wortes aabb simuliert.
Man erhält schließlich die folgende Situation:
q1; Z | λ,Z;λ q2
Wenn das gesamte Eingabewort abgearbeitet ist, befindet sich der Kellerautomat im
Zustand q1 mit der Symbolfolge Z im Keller (also: mit einem leeren Keller).
Mit dem Zustandsübergang q1 - λ,Z;λ -> q2 gelangt der Kellerautomat schließlich in
den Endzustand.
Das Verfahren lässt sich auf alle Wörter der Sprache Lab anwenden.
Wenn ein Eingabewort nicht zur Sprache Lab gehört - also nicht mit den Produktionen
der Grammatik G abgeleitet werden kann, dann lassen sich nicht sämtliche Nichtterminalsymbole
mit Hilfe geeigneter Zustandsübergänge aus dem Keller entfernen. Da sich der Keller somit nicht leeren lässt,
kann der letzte Zustandsübergang in den Endzustand nicht erfolgen. Mit entsprechenden verallgemeinernden
Überlegungen erhält man den folgenden Satz.
Satz (über den Zusammenhang zwischen kontextfreien Sprachen und nichtdeterministischen Kellerautomaten):
Zu jeder kontextfreien Sprache gibt es einen nichtdeterministischen Kellerautomaten,
der diese Sprache erkennt. Der Kellerautomat kann
automatisiert aus einer kontextfreien Grammatik zur kontextfreien Sprache erzeugt werden.
Vom Kellerautomaten zur kontextfreien Grammatik
Auch die umgekehrte Übersetzung ist möglich. Als Beispiel betrachten wir den folgenden Kellerautomaten zur Erkennung der Sprache Lab = {anbn | n = 1, 2, 3, ...}.

Um ihn mit Hilfe von JFlap automatisiert in eine Grammatik übersetzen zu können, muss der
Zustandsübergang q1 - λ,S;aSb -> q1 durch die beiden Zustandsübergänge
q1 - λ,S;Xb -> q3 - λ,X;aS -> q1 ersetzt werden.
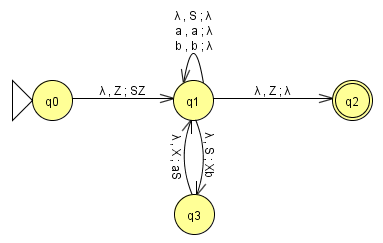
Zu diesem Kellerautomaten lässt sich die folgende Grammatik zur Sprache Lab = {anbn | n = 1, 2, 3, ...} automatisiert erzeugen:
S -> LD A -> a B -> b L -> FB D -> λ F -> AL L -> λ
Der Zusammenhang zwischen Kellerautomat und zugehöriger Grammatik ist nicht direkt zu durchschauen und soll hier auch nicht weiter analysiert werden. Folgender Satz lässt sich aber allgemein zeigen:
Satz (über den Zusammenhang zwischen nichtdeterministischen Kellerautomaten und kontextfreien Sprachen):
Die Sprache eines nichtdeterministischen Kellerautomaten ist kontextfrei:
Zum nichtdeterministischen Kellerautomaten gibt es eine kontextfreie Grammatik, die dieselbe Sprache
erzeugt, die vom Kellerautomaten erkannt wird. Man kann diese kontextfreie Grammatik automatisiert erzeugen.
Deterministische und nichtdeterminische Kellerautomaten
Im Kontext Endliche Automaten
haben wir gesehen, dass deterministische und nichtdeterministische
endliche Automaten gleichmächtig sind. Mit beiden Automatentypen können dieselben (regulären) Sprachen
erkannt werden.
Für Kellerautomaten gilt ein analoger Sachverhalt nicht. Nichtdeterministische Kellerautomaten sind mächtiger als deterministische Kellerautomaten. Es gibt also kontextfreie Sprachen, die zwar von nichtdeterministischen, nicht jedoch von deterministischen Kellerautomaten erkannt werden. Ein Beispiel für eine solche Sprache wird durch folgende Grammatik festgelegt.
S -> 0S0 S -> 1S1 S -> λ
Grenzen von Kellerautomaten
Wir haben gesehen, dass nichtdeterministische Kellerautomaten genau die kontextfreien Sprachen erkennen.
Es gibt Sprachen, die nicht mit einer kontextfreien Grammatik beschrieben werden können. Die Sprache LMyXML gehört zu diesen Sprachen. Die folgende Grammatik zu dieser Sprache enthält Produktionen, die nicht kontextfrei sind. Man kann beweisen, dass es keine Grammatik zu dieser Sprache gibt, die ausschließlich aus kontextfreien Produktionen besteht.
S ->S -> T -> aAT T -> bBT T -> M Aa -> aA Ab -> bA AM -> Ma Ba -> aB Bb -> bB BM -> Mb M -> >N M -> aM M -> bM M -> cM M -> Aus den beiden Aussagen folgt jetzt, dass z.B. die Sprache LMyXML nicht von einem (noch so komplizierten) nichtdeterministischen Kellerautomaten erkannt werden kann.
Genau wie dem Verarbeitungsmodell
endlicher Automatsind auch dem VerarbeitungsmodellKellerautomatsomit Grenzen gesetzt.

