Theorie - Reguläre Ausdrücke und endliche Automaten
Reguläre Ausdrücke
Reguläre Ausdrücke dienen dazu, Sprachen zu beschreiben. So lässt sich die Sprache
LBin = {0, 1, 10, 11, 100, 101, 110, 111, 1000, ...}
mit Hilfe des folgenden regulären Ausdruckes beschreiben:
0+1(0+1)*
Zur Erinnerung: Reguläre Ausdrücke über dem Alphabet Σ
werden wie folgt definiert:
-
Øist ein regulärer Ausdruck. -
λist ein regulärer Ausdruck. -
Für jedes
a ∈ Σistaein regulärer Ausdruck. -
Wenn
αundβreguläre Ausdrücke sind, dann sind auch die Konkatenationαβ, die Alternativeα+βund die Iteration(α)*reguläre Ausdrücke.
Ein Automatenbaukasten
Zu einem regulären Ausdruck kann man recht einfach einen endlichen Automaten konstruieren, der die vom regulären Ausdruck beschriebene Sprache akzeptiert. Der Automat kann dabei aus den Bestandteilen des regulären Ausdrucks nach dem Baukastenprinzip konstruiert werden. Im Folgenden wird erst einmal der Automatenbaukasten vorgestellt.
Zum regulären Ausdruck Ø gehört der folgende endliche Automat:
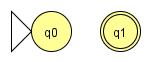
Zum regulären Ausdruck λ gehört der folgende endliche Automat:
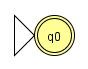
Zum regulären Ausdruck a mit a ∈ Σ gehört der folgende endliche Automat:
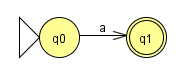
Wenn A1 ein endlicher Automat für den regulären Ausdruck α ist und
A2 ein endlicher Automat für den regulären Ausdruck β, dann kombiniert
man diese beiden endlichen Automenten wie folgt zu einem für den regulären Ausdruck αβ:
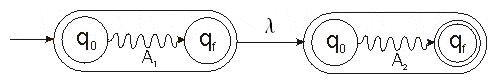
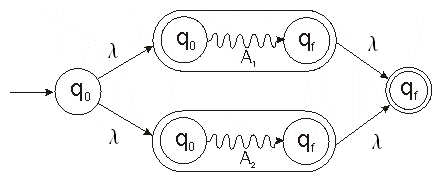
Wenn A1 ein endlicher Automat für den regulären Ausdruck α ist und
A2 ein endlicher Automat für den regulären Ausdruck β, dann kombiniert
man diese beiden Automenten wie folgt zu einem für den regulären Ausdruck α+β:
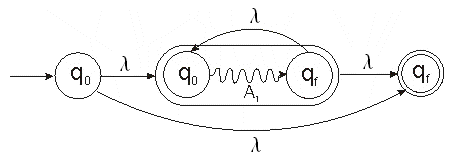
Wenn A1 ein endlicher Automat für den regulären Ausdruck α ist, dann erhält
man wie folgt einen endlichen Automaten zum regulären Ausdruck (α)*:
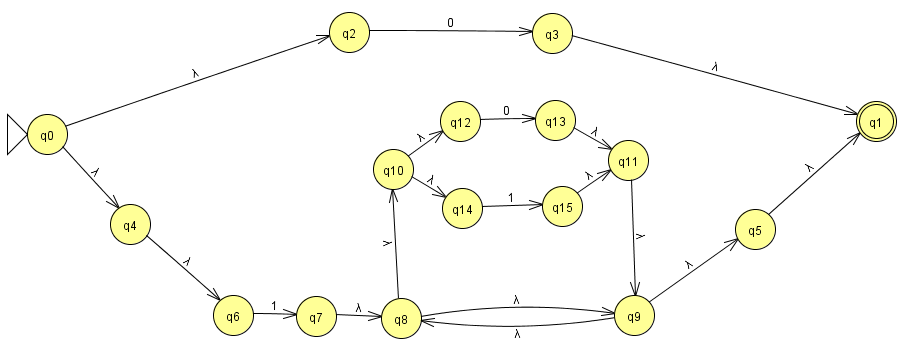
Wenn man die vorgestellten Konstruktionsregeln befolgt, dann ergibt sich der folgende endliche Automat
zum regulären Ausdruck 0+1(0+1)*:
Theorie
Die Vorüberlegungen deuten darauf hin, dass es Zusammenhänge zwischen endlichen Automaten und regulären Ausdrücken gibt.
Satz (über den Zusammenhang zwischen regulären Ausdrücken und (nicht)deterministischen endlichen Automaten):
Zu jedem regulären Ausdruck gibt es einen nichtdeterministischen endlichen Automaten (und folglich auch einen
deterministischen endlichen Automaten), der die vom regulären Ausdruck beschriebene Sprache erkennt.
Der (nicht)deterministische endliche Automat kann
automatisiert aus dem regulären Ausdruck erzeugt werden.
Auch die umgekehrte Erzeugung ist möglich:
Satz (über den Zusammenhang zwischen (nicht)deterministischen endlichen Automaten und regulären Ausdrücken):
Zu jedem nichtdeterministischen endlichen Automaten (und folglich auch
deterministischen endlichen Automaten) gibt es einen regulären Ausdruck, der die vom
(nicht)deterministische endlichen Automaten erkannte Sprache beschreibt.
Der reguläre Ausdruck kann
automatisiert aus dem endlichen Automaten erzeugt werden.
Fasst man die Ergebnisse aus diesem und dem vorangegangenen Abschnitt zusammen, so erhält man den folgenden fundamentalen Satz:
Satz (über reguläre Sprachen und endliche Automaten):
Die Klasse der Sprachen, die mit einer regulären Grammatik beschrieben werden können,
ist identisch mit der Klasse der Sprachen, die mit einem regulären Ausdruck beschrieben werden können.
Sie ist ebenso identisch mit der Klasse der Sprachen, die von deterministischen endlichen Automaten bzw.
von nichtdeterministischen endlichen Automaten erkannt werden können.

