Kann ein Akzeptor alle Sprachen erkennen?
Die Klammersprache
Gegeben sei die durch das folgende Syntaxdiagramm definierte formale Sprache der (stark vereinfachten) Klammerausdrücke. Sie enthält beispielsweise die folgenden Wörter:
Sie enthält beispielsweise die folgenden Wörter:
(), (()), (((((()))))).
Zur Sprache gehören also alle Klammerausdrücke, bei denen nach einer Folge öffnender Klammern genau so viele schließende Klammern folgen. Diese Sprache wird oft auch etwas abstrahierend in der Form anbn dargestellt.
Die öffnenden Klammern werden durch das Symbol a repräsentiert, die schließenden
Klammern durch das Symbol b. Entscheidend ist auch hier, dass die Anzahl der
schließenden Klammern genau der Anzahl der öffnenden Klammern entspricht.
Gibt es einen endlichen Automaten, der die Sprache anbn erkennt?
Versuche, einen solchen endlichen Automaten zu konstruieren, scheitern an der Schwierigkeit,
die Anzahl der öffnenden Klammern im Automaten mitzuzählen
.
Es scheint, dass diese Schwierigkeit bei endlichen Automaten - die ja eine feste Anzahl von Zuständen haben -
unüberwindbar ist.
Die folgende Argumentation zeigt, dass das tatsächlich der Fall ist.
Wir benutzen dabei einen Beweis durch Widerspruch. Wir nehmen an, dass es einen Automaten A gibt,
der die Sprache der Klammerausdrücke erkennt und führen diese Annahme dann
zu einem Widerspruch. Die Annahme muss folglich falsch sein.
Der Beweis
Angenommen, es gibt einen endlichen Automaten A, der anbn erkennen kann.
Dieser Automat A hat - da er endlich ist - eine feste Anzahl von Zuständen, etwa m = 10 (die Zahl 10 ist hier willkürlich gewählt, die Argumentation funktioniert auch mit jeder anderen Zahl).
Wir wählen nun ein Wort akbk mit k > m, etwa k = 12.
Bei der Abarbeitung des Wortes a12b12 muss bereits bei der Verarbeitung der 12 a's auf jeden Fall ein Zustand Zx mindestens zweimal durchlaufen werden, denn es gibt mehr a's als Zustände.
Wir nehmen einmal an, dass der Zustand Zx mit dem dritten a und mit dem siebten a erreicht wird.
Für die folgende Argumentation ist nicht entscheidend, mit welchen a's man Zx erreicht, sondern
nur, dass Zx zweimal durchlaufen wird.
Es entsteht eine Schleife, die erst mit dem ersten b wieder verlassen wird.
Wie die 12 b's den Automaten in einen Endzustand bringen, ist für die Argumentation ohne Belang.
Eine mögliche Konstellation zeigt das folgende Bild:
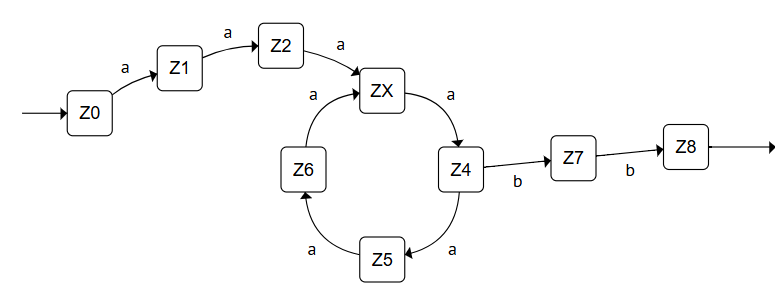
Dem Bild kann man direkt entnehmen, dass neben a12b12 auch andere Wörter wie a8b12 (Schleife wurde einmal durchlaufen) oder auch a16b12 (Schleife wurde dreimal durchlaufen) akzeptiert werden.
Der Automat akzeptiert folglich auch Wörter, die nicht zu anbn gehören. Das steht aber im Widerspruch zur Annahme, dass anbn die Sprache des Automaten ist. Die Annahme mussfolglich falsch gewesen sein.
Ein endlicher erkennener Automat (Akzeptor) kann die Sprache anbn nicht erkennen. Das liegt daran, dass diese Sprache nicht regulär ist. Allgemein können Akzeptoren nur reguläre Sprachen erkennen.
Um nicht reguläre Sprachen zu erkennen, braucht es eine Erweitertung des Modells "endlicher Automat". Diese Erweiterungen findest du in den folgenden Kapiteln.
Da die Sprache anbn nicht regulär ist, gibt es auch keinen regulären Ausdruck, der sie definiert. Die Klammersprache bzw. die Sprache anbn kann jedoch mit einem Syntaxdiagramm (wie auf dieser Seite oben geschehen) definiert werden.

