Anwendung - Streckenzüge
Geometrische Figuren als Streckenzüge
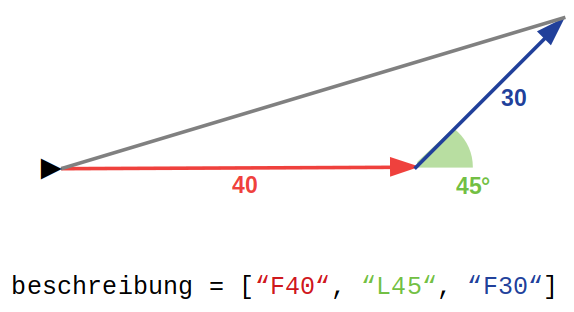
In den folgenden Aufgaben geht es um die Verwaltung geometrischer Figuren. Eine Figur wird dabei als geschlossener Streckenzug festgelegt, d.h. als Folge von Anweisungen der folgenden Art:
-
F: Gehe um eine bestimmte Anzahl Längeneinheiten vorwärts. -
L: Drehe dich um eine bestimmte Gradzahl nach links. -
R: Drehe dich um eine bestimmte Gradzahl nach rechts.
Nach Abarbeiten der Anweisungen wird der Streckenzug (auch ohne explizite Anweisung) geschlossen, d.h. eine Verbindung zum Startpunkt gezogen.
Beispiel:
Im Folgenden wird das Python-Modul turtle verwendet. Ein Überblick dazu befindet sich im Kapitel
Exkurs - Turtle-Grafik.
Aufgabe 1
(a) Teste das vorgegebene Programm. Was bedeuten die einzelnen Parameter des Konstruktors der Klasse Streckenzug?
(b) Erweitere die Szene um einen weiteren Baum bestehend aus einem Rechteck und einem Dreieck.
from turtle import *
# Klasse Streckenzug
class Streckenzug(object):
def __init__(self, start, beschreibung):
self.start = start
self.beschreibung = beschreibung
def __str__(self):
text = "Streckenzug bei (" + str(self.start[0]) + "|" + str(self.start[1]) + "), " + str(self.start[2]) + "°"
return text
def zeichnen(self):
penup()
goto(self.start[0], self.start[1])
setheading(self.start[2])
pendown()
for angabe in self.beschreibung:
befehl = angabe[0]
wert = float(angabe[1:])
if befehl == "F":
forward(wert)
elif befehl == "L":
left(wert)
elif befehl == "R":
right(wert)
goto(self.start[0], self.start[1])
setheading(self.start[2])
# Zeichnen der Szene
reset()
speed(0)
z = Streckenzug((-80, -100, 90), ["L40", "F120", "R40", "F40", "R110", "F100"])
r = Streckenzug((-90, -10, 90), ['F20', 'L90', 'F40', 'L90', 'F20'])
d = Streckenzug((-100, 30, 90), ['F40', 'L100', 'F100'])
s1 = Streckenzug((70, 250, 90), ['R20', 'F30', 'R140', 'F30', 'L50', 'F30', 'R140', 'F30', 'L50', 'F30', 'R140', 'F30', 'L50', 'F30', 'R140'])
s2 = Streckenzug((-40, 220, 90), ['R20', 'F30', 'R140', 'F30', 'L50', 'F30', 'R140', 'F30', 'L50', 'F30', 'R140', 'F30', 'L50', 'F30', 'R140'])
n = Streckenzug((0, 0, 90), ['F100', 'L135', 'F141.4', 'L225', 'F100', 'L135', 'F70.7', 'L90', 'F70.7', 'L45', 'F100', 'L135', 'F141.4', 'L225', 'F100'])
figuren = [z, r, d, s1, s2, n]
for figur in figuren:
figur.zeichnen()
Aufgabe 2
Die Klasse Rechteck erbt von Streckenzug:
# Klasse Streckenzug
class Streckenzug(object):
...
# Klasse Rechteck
class Rechteck(Streckenzug):
def __init__(self, start, a, b):
self.breite = a
self.laenge = b
beschreibung = ["F" + str(self.breite), "L90", "F" + str(self.laenge), "L90", "F" + str(self.breite)]
Streckenzug.__init__(self, start, beschreibung)
def __str__(self):
text = "Rechteck bei (" + str(self.start[0]) + "|" + str(self.start[1]) + "), " + str(self.start[2]) + "°"
return text
def getBreite(self):
return self.breite
def getLaenge(self):
return self.laenge
(a) Erzeuge einige Objekte der Klasse Rechteck.
(b) Ergänze Methoden zur Berechnung von Flächeninhalt und Umfang des Rechtecks (Vgl. Klassendiagramm).
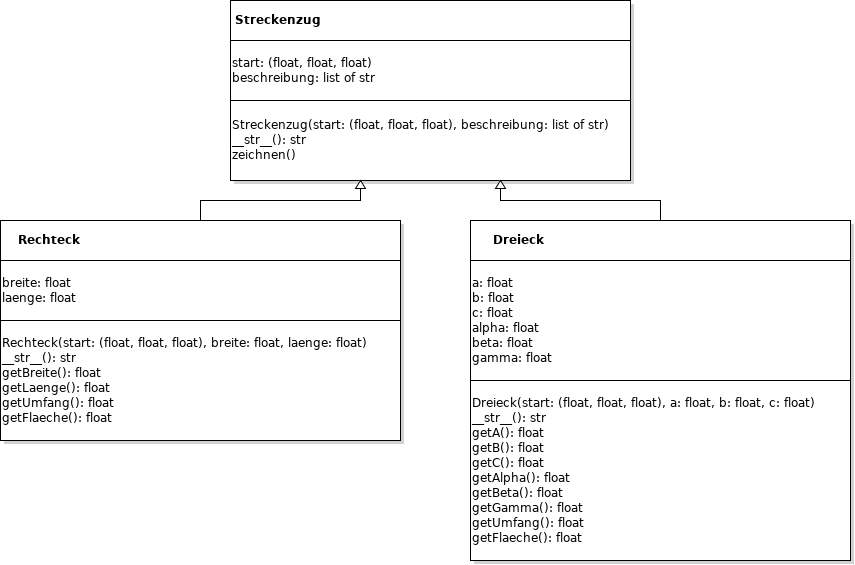
(c) Entwickle entsprechend die Klasse Dreieck, welche von Streckenzug erbt. Hierzu einige Tipps:
- Berechnung eines Winkels (hier Alpha) mit Hilfe des Kosinussatzes in Python:
alpha = degrees(acos((b * b + c * c - a * a) / (2 * b * c))). Damit dies funktioniert, musst dufrom math import *dem Programm voranstellen. - Eine Formel zur Berechnung der Dreiecksfläche aus den drei Seitenlängen findest du hier.
Aufgabe 3
Entwickle weitere Klassen, welche von Streckenzug erben. Hier einige Vorschläge:
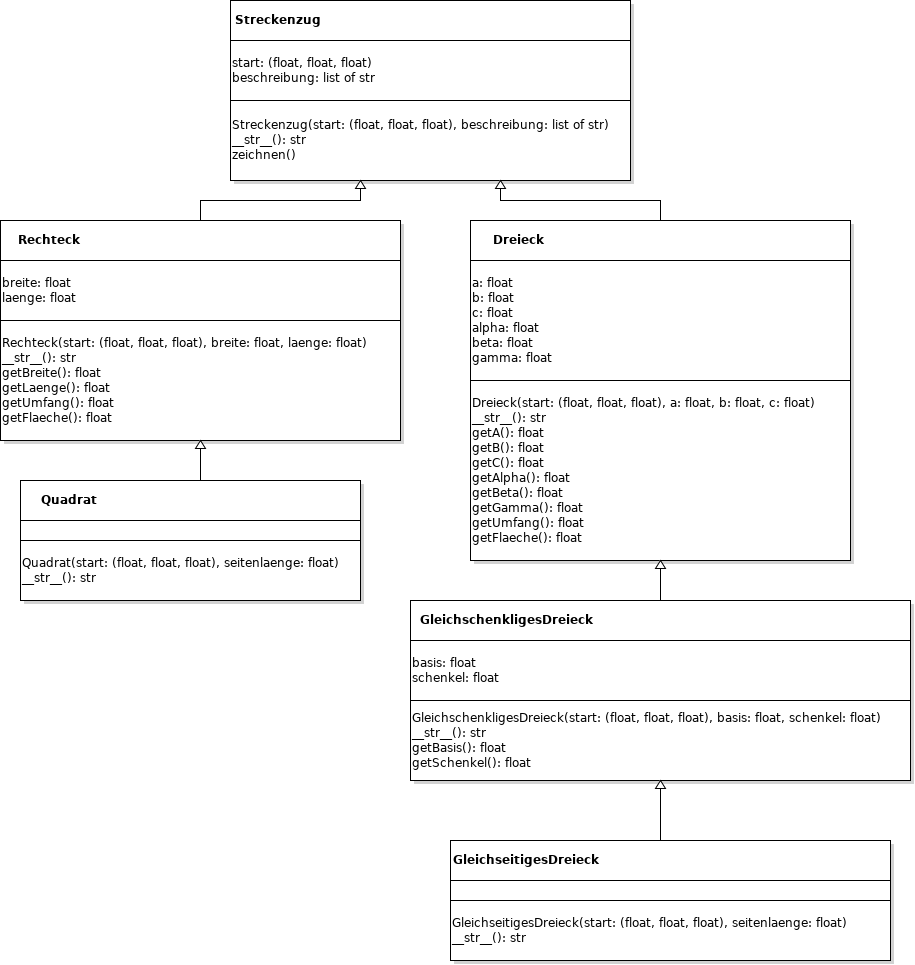
Orientiere dich bei folgenden Aufgaben am untenstehenden Klassendiagramm.
(a) Entwickle eine Klasse Quadrat, welche von Rechteck erbt.
(b) Entwickle eine Klasse GleichschenkligesDreieck, welche von Dreieck erbt sowie eine Klasse GleichseitigesDreieck, welche von GleichschenkligesDreieck erbt.
(c) Verdeutliche am Klassendiagramm die Begriffe Spezialisierung und Generalisierung.
Quellen
- [1]: Streckenzug - Urheber: JJ - Lizenz: inf-schule.de