XOR-Problem
Die so gennante XOR-Funktion $y=x_1 \underline{\lor} x_2 = (x_1 \land \overline{x}_2 ) \lor (\overline{x}_1 \land x_2)$ ist durch ein einzelnes Perzeptron nicht modellierbar, wie man sofort anhand der folgenden Abbildung erkennen kann:
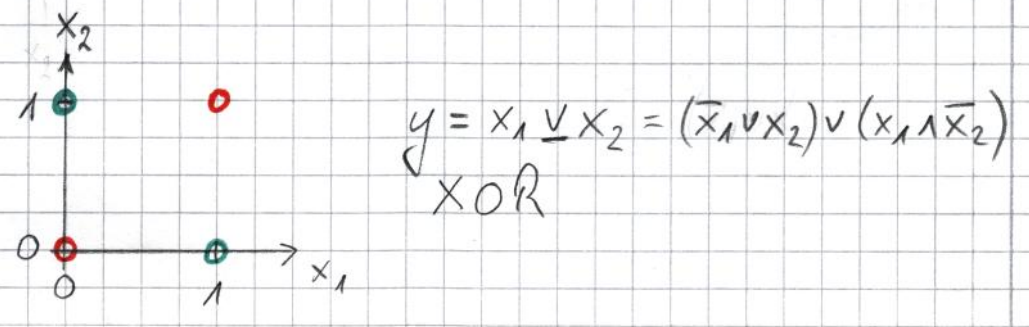
Die grün eingezeichneten Punkte sind von den rot eingezeichneten Punkten nicht durch eine Gerade separierbar, so dass sich die XOR-Funktion nicht mittels eines einzelnen Perzeptrons modellieren lässt.
Das XOR-Problem kann dennoch mittels Perzeptronen beschrieben werden, indem mehrere einzelnen Perzeptronen wie folgt zu einem so genannten mehrlagigen Perzeptron zusammengeschaltet werden.

Die Abbildung zeigt ein mehrlagiges Perzeptron zur Modellierung der XOR-Funktion $y=x_1 \underline{\lor} x_2$. Beachte, dass die beiden so genannten Eingangsperzeptronen im strengeren Sinne gar keine echten Perzeptronen sind, da sie lediglich ihre Eingangswerte unverändert an die nächste Schicht von Perzeptronen weiterleiten.
Die Ausgänge der beiden so genannten Eingangsperzeptronen leiten dabei die an ihren Eingängen anliegenden Werte $x_1$ bzw. $x_2$ unverändert weiter an die Eingänge dreier Perzeptronen in einer verborgenen Schicht, einem so genannten hidden layer. Die Ausgänge der Perzeptronen des hidden layers wiederum stellen die drei Eingänge des Ausgabeperzeptrons dar.
Durch Ausprobieren aller vier möglichen Eingangkonfigurationen stellt man fest, dass dieses mehrlagige Perzeptron das XOR-Problem löst, dass also gilt:
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Aufgabe 1
Entwickle ein eigenes mehrlagiges Perzeptron für das XOR-Problem, indem du geschickt die in diesemfrüheren Kapitel entwickelten "logischen" Perzeptronen kombinierst. Zeichne das entwickelte mehrlagige Perzeptron als Baumdiagramm inklusive der Gewichte und der Schwellenwerte. In dem folgenden Unterkapitel kannst du dein mehrlagiges Perzeptron dann mit einem Jupyter-Notebook testen.Aufgabe 2
Modelliere die Funktion $y=\overline{x_1 \underline{\lor} x_2} = (x_1 \land x_2 ) \lor (\overline{x}_1 \land \overline{x}_2)$, also| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

