Verwendung von Hilfsfunktionen

Verständlichkeit als Ziel

Wir betrachten weiterhin das folgende Hausmodell.

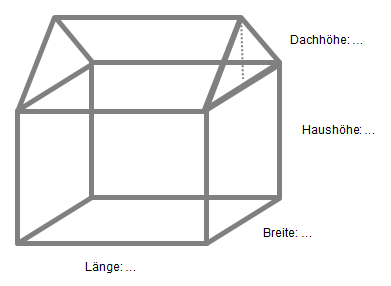
Zur Berechnung der gesamten Oberfläche des Hauses (ohne den Boden) haben wir im letzten Abschnitt die folgende Funktion(sdefinition) entwickelt:

from math import sqrt

def flaecheHaus(laenge, breite, hoeheHaus, hoeheDach):
    return 2*laenge*hoeheHaus + \
           2*breite*hoeheHaus + \
           2*(breite*hoeheDach/2) + \
           2*laenge*sqrt((breite/2)*(breite/2)+hoeheDach*hoeheDach)

Der Berechnungsausdruck innerhalb der Funktionsdefinition ist hier bereits recht komplex. Meist ist es schwierig, komplexe Berechnungsausdrücke korrekt zu entwickeln. Schwierig ist es zudem, komplexe Berechnungsausdrücke nachträglich zu durchschauen. In der Informatik nutzt man in solchen Situationen Strategien zur Reduzierung der Komplexität. Man zerlegt das Berechnungsproblem in überschaubare Teilprobleme und führt Hilfsfunktionen zur Bearbeitung der Teilprobleme ein. Wir spielen das im Folgenden im aktuellen Kontext einmal durch.

Konzeption von Hilfsfunktionen

Wenn man beliebige Berechnungen für Hausoberflächen durchführen möchte, muss man jeweils die Flächeninhalte von Rechtecken und Dreiecken sowie die Länge der Hypotenuse in einem rechtwinkligen Dreieck berechnen. Es ist günstig, für solche Teilberechnungen Hilfsfunktionen einzuführen.

Funktion zur Berechnung des Flächeninhaltes eines Rechtecks:

Funktion zur Berechnung des Flächeninhaltes eines Dreiecks:

Funktion zur Berechnung der Länge der Hypotenuse in einem rechtwinkligen Dreieck:

Aufgabe 1

Ergänze die fehlenden Funktionsdefinitionen und teste sie mit Funktionsaufrufen.

Verwendung der Hilfsfunktionen

Wir entwickeln zunächst eine Funktion zur Berechnung des Flächeninhalts einer Giebelfläche (das ist die gesamte Seitenfläche).

Diese Funktion kann man jetzt mit den bereits entwickelten Hilfsfunktionen so definieren:

def flaecheGiebel(breite, hoeheHaus, hoeheDach):
    return flaecheRechteck(breite, hoeheHaus) + \
           flaecheDreieck(breite, hoeheDach)

Aufgabe 2

(a) Entwickle analog Black-Box-Modellierungen und Funktionsdefinitionen für die Funktionen flaecheDach (für die gesamte Dachfläche) und flaecheSeitenwaende (für die Vorder- und Rückseite des Hauses).

(b) Entwickle anschließend eine Black-Box-Modellierung und eine Funktionsdefinition für die Funktion flaecheHaus (für die gesamte Oberfläche des Hauses). Benutze hier die neu entwickelten Hilfsfunktionen. Bestimme mit dieser Funktion den Materialbedarf für die im letzten Abschnitt angegebenen Maße.

(c) Erläutere, warum es günstig ist, Hilfsfunktionen einzuführen und sie bei der Definition der eigentlich benötigten Funktion zu benutzen.