Entwicklung eines Addiersystems - verschiedene Ansätze

Addieren in verschiedenen Zahlensystemen

Sicherlich hast du schon gemerkt, dass das Addieren so fundamental ist, weil man alle mathematischen Grundoperationen auf das Addieren zurückführen kann. So ist die Subtraktion eine umgekehrte Addition (2. Summand mit negativem Vorzeichen). Die Multiplikation dagegen ist eine wiederholte Addition und die Division - sofern man bei zunächst ganzen Zahlen bleibt - ist eine wiederholte Subtraktion.

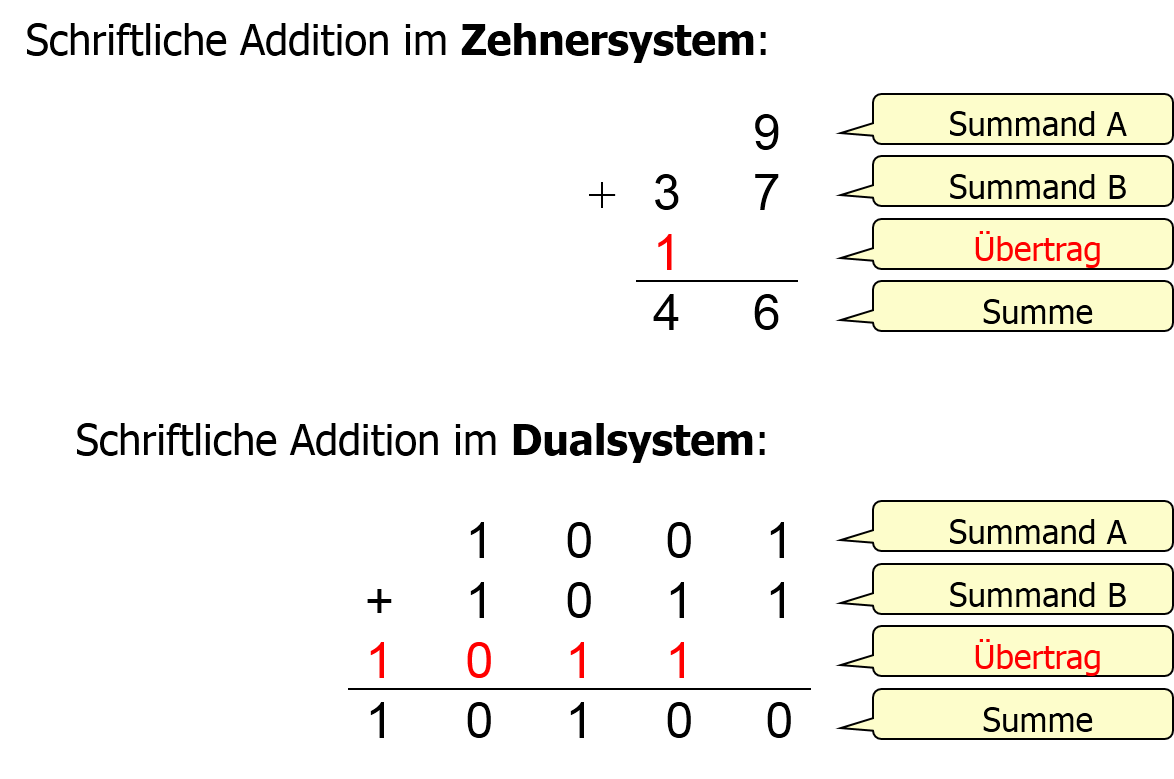
Beim Addieren ist darauf zu achten, in welchem Zahlensystem man rechnet (s. Binärdarstellung ). So ist in unserem alltäglichen Dezimalsystem 1 + 1 = 2 aber im Dualsystem dagegen gilt 1 + 1 = 0 mit Übertrag 1. Weiterhin ist 1 + 1 + 1 = 1 mit Übertrag 1. Falls du mit dem Rechnen von Dualzahlen noch nicht ganz vertraut bist, schaue dir einfach das Kapitel Binärdarstellung an.

 

Damit erhält man für die vorangegangene Addition:

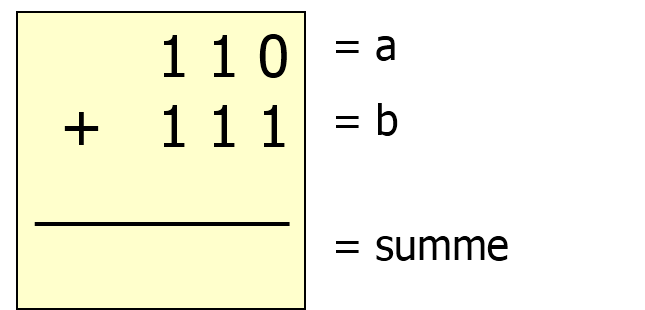
Ziel soll es nun sein, eine Addierschaltung für zwei Dualzahlen a und b mit je 3 Bit (also a0, a1, a2 und b0, b1, b2) zu erstellen:

Aufgabe 1

(a) Berechne das Ergebnis des Beispiels.

(b) Bestimme, wie viele Bits allgemein für die Summe benötigt werden, wenn zwei 3 Bit Zahlen addiert werden.

(c) Wie viele Bits werden für die Summe benötigt werden, wenn zwei 32 Bit Zahlen addiert werden?

Ansatz 1: Eine Wertetabelle

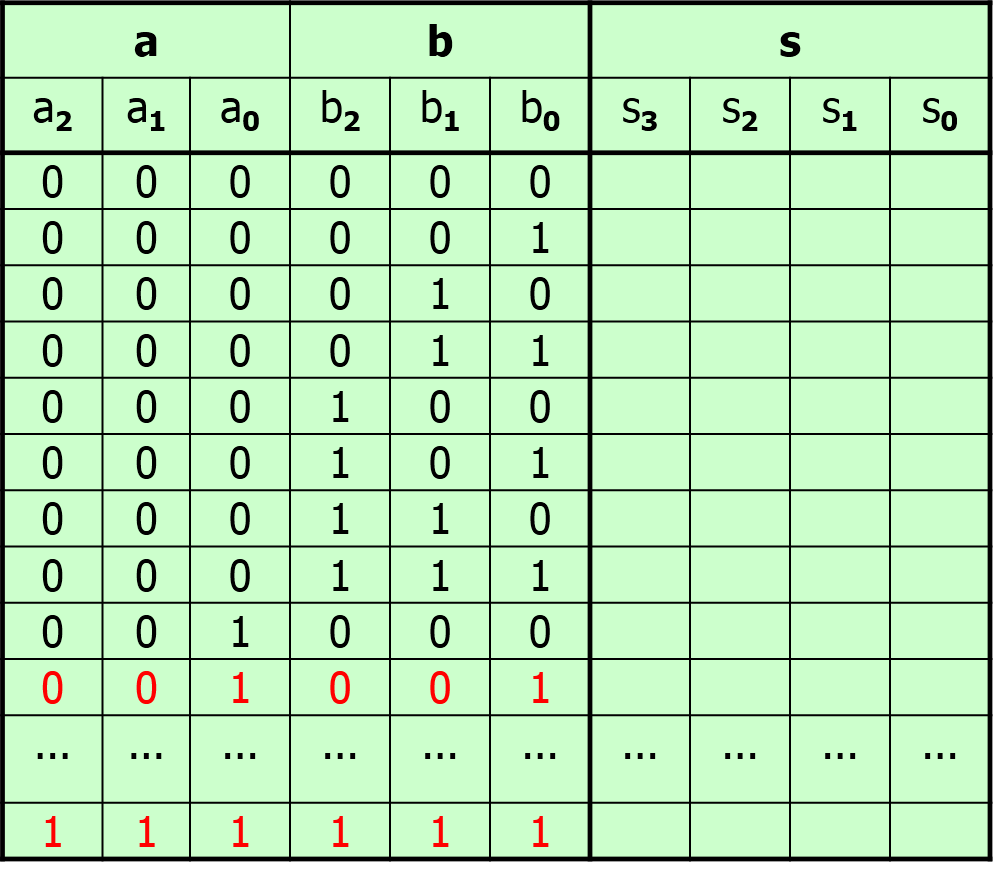
Eine Schaltung mit je 3 Bit ergibt eine Summe von 4 Bit (s0, s1, s2, s3). Beachte, dass s3 das höchststellige Bit, $2^3$, ist.

Ein erster Ansatz ist daher, die gewünschte Addition mit einer Wertetabelle zu lösen. Dabei wird für jede Möglichkeit das Ergebnis berechnet. Man geht dabei systematisch nach dem Dualsystem vor.

Aufgabe 2

(a) Berechne die Ergebnisse der letzten beiden notierten Zeilen (rot).

(b) Aus wie vielen Zeilen besteht die Tabelle insgesamt? Erkläre.

(c) Wie ändert sich die Gesamtzahl der Zeilen bei Addition zweier 64-Bit Zahlen? Begründe.

Ansatz 2: Ein ROM-Speicher

Das Vervollständigen der Wertetabelle ist dir sicherlich nicht schwer gefallen. Die fertige Tabelle findest du hier. Bei 6 Eingangsvariablen sind das $2^6 = 64$ Kombinationen. Betrachtet man heutige 64-Bit Betriebssysteme sind das $2 \cdot 64$ also 128 Eingangsvariablen und damit $2^{128} = 3,4 \cdot 10^{38}$ Kombinationen! Das sind zu viele Zeilen bis man das Ergebnis findet...
Versuchen wir einen anderen Ansatz: Die gewünschten Werte der Tabelle werden zuvor in einem ROM-Baustein („read-only-memory“) fest gespeichert („eingebrannt“). Die Eingangsbits von a und b werden dann als Adresse benutzt und der Speicher liefert jeweils das zugehörige Ergebnis.

Aufgabe 3

(a) Wie „groß“ wäre ein ROM für zwei 3-Bit-Zahlen?

(b) Wie groß wäre er für zwei 16-Bit-Zahlen?